Question
Question: How do you write the equation for a hyperbola given vertices \(\left( -5,0 \right)\) and \(\left( 5,...
How do you write the equation for a hyperbola given vertices (−5,0) and (5,0), conjugate axis of length 12 units?
Solution
In this problem we need to calculate the equation of the hyperbola with a given vertex and conjugate axis length. On observing the vertices, we have the same y coordinates, so the hyperbola is horizontal transverse axis type. For this we will assume the equation of the hyperbola as a2(x−h)2−b2(y−k)2=1. From this equation we can write the coordinates of the vertices and equate them with the given values to get the values of h, k, a. Now we will equate the length of the conjugate axis to 2b and simplify the equation to get the value of b. Now we will substitute all the values we have in the equation of hyperbola to get the required result.
Complete step by step answer:
Given that, (−5,0) and (5,0) are the vertices of the hyperbola and the length of the conjugate axis is 12 units.
We can observe that the y coordinates of the given vertices are equal. So, the hyperbola is a horizontal transverse axis type. Hence assume the equation of the hyperbola as
a2(x−h)2−b2(y−k)2=1.
For the above hyperbola the coordinates of vertices will be (h+a,k), (h−a,k). Comparing these values with the values of given vertices, then we will get
k=0, h+a=5, h−a=−5.
Solving the equations h+a=5, h−a=−5, then we will get
h=0, a=5.
Now the length of the conjugate axis of the hyperbola is 2b. Equating this value with the given conjugate axis length then we will have
⇒2b=12⇒b=6
Substituting the all the values we have in the equation of the hyperbola, then we will get
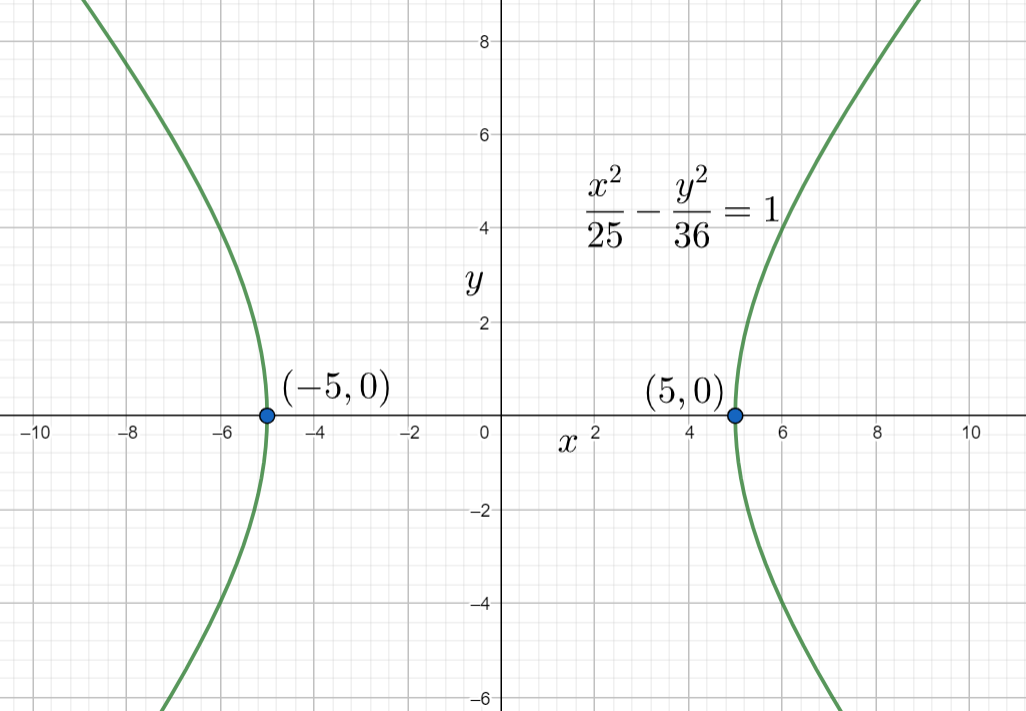
⇒52(x−0)2−62(y−0)2=1⇒52x2−62y2=1
Hence the equation of the required hyperbola is 25x2−36y2=1 and the diagram of the hyperbola is given by
Note:
In this problem we have the y coordinates of the vertices are same so we have assumed the equation of the hyperbola as a2(x−h)2−b2(y−k)2=1. If we have the x coordinates of the vertices are same then we need to assume the equation of the hyperbola as b2(y−k)2−a2(x−h)2=1.
