Question

How do you write the equation for a circle where the points $\left( 2,6 \right)$and $\left( 8,10 \right)$ lie along a diameter? $$$$

Answer 1

We use the standard equation of circle with centre $\left( a,b \right)$ and radius $r$ that is ${{\left( x-a \right)}^{2}}+{{\left( y-b \right)}^{2}}={{r}^{2}}$. We find the centre $\left( a,b \right)$of the circle using midpoint formula of two points $\left( {{x}_{1}},{{y}_{1}} \right),\left( {{x}_{2}},{{y}_{2}} \right)$ as $\left( \dfrac{{{x}_{1}}+{{x}_{2}}}{2},\dfrac{{{y}_{1}}+{{y}_{2}}}{2} \right)$. We use distance formula between two points that is $d=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}$ to find length of the diameter. We take half of diameter to get the radius $r$.$$$$

Complete step by step answer:
We know that if $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$ are two distinct points in plane then the coordinates of the midpoint of the line segment joining them is given by $\left( \dfrac{{{x}_{1}}+{{x}_{2}}}{2},\dfrac{{{y}_{1}}+{{y}_{2}}}{2} \right)$ and the distance between them is given by
$d=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}$
We also know the standard equation of the circle in $xy-$plane with centre $\left( a,b \right)$ and radius $r$ is given by
${{\left( x-a \right)}^{2}}+{{\left( y-b \right)}^{2}}={{r}^{2}}$

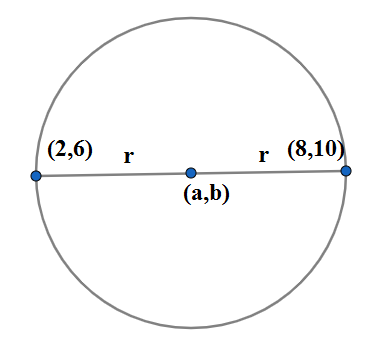
We are given in the question the coordinates of two endpoints of diameter $\left( 2,6 \right)$and $\left( 8,10 \right)$. We know that the midpoint of the diameter is the centre of the circle. We use midpoint formula on the given endpoints of the diameter and find the centre as
$\left( \dfrac{2+8}{2},\dfrac{10+6}{2} \right)=\left( \dfrac{10}{2},\dfrac{16}{2} \right)=\left( 5,8 \right)$
We use the distance formula between two points and find the length of the diameter as
$d=\sqrt{{{\left( 8-2 \right)}^{2}}+{{\left( 10-6 \right)}^{2}}}=\sqrt{{{6}^{2}}+{{4}^{2}}}=\sqrt{52}=2\sqrt{13}$
We know that the length of the radius is half diameter. So we have radius as
$r=\dfrac{d}{2}=\dfrac{2\sqrt{13}}{2}=\sqrt{13}$
We put centre $\left( a,b \right)=\left( 5,8 \right)$and radius $r=5$in the standard equation to have the required equation of circle as

& {{\left( x-5 \right)}^{2}}+{{\left( y-8 \right)}^{2}}={{\left( \sqrt{13} \right)}^{2}} \\\ & \Rightarrow {{\left( x-5 \right)}^{2}}+{{\left( y-8 \right)}^{2}}=13 \\\ \end{aligned}$$ **Note:** We note that the general equation of circle in two variables is given by ${{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0$ where the centre is given by $\left( -g,-f \right)$ and the radius is given by $r=\sqrt{{{g}^{2}}+{{f}^{2}}-c}$. We can expand the obtained equation of the circle in centre-radius form to two variable forms as ${{x}^{2}}+{{y}^{2}}-10x-16y-76=0$. We can also find the radius by using the distance formula from centre $\left( 5,8 \right)$ to one of the endpoints $\left( 2,6 \right)$and $\left( 8,10 \right)$.