Question

How do you write the definite integral to find the smaller area cut from the circle ${{x}^{2}}+{{y}^{2}}=25$ by the line $x=3$ ?

Answer 1

In this question, we have to find the area of a definite integral. Thus, we will use an area of integrals to get the solution for the problem. So, we will first draw the graph of the equation of a circle and the equation of the line. Thus, we will see that the line cut the circle into two parts, one is bigger and another one is smaller. Thus, for the problem, we have to write the definite integral for the smaller area cut. Therefore, we will change the equation of a circle in terms of x and get the range of x, to get the required solution for the problem.

Complete step-by-step solution:
According to the question, we have to find the definite integral from a circle and the line.
Thus, we will use the area of integrals method to get the solution.
The equation of a circle and the line is given to us is ${{x}^{2}}+{{y}^{2}}=25$ and $x=3$ respectively --- (1)
We will first draw the graph of the circle ${{x}^{2}}+{{y}^{2}}=25$ and the line $x=3$ , thus get a smaller area, which we have to find for the definite integral, we get

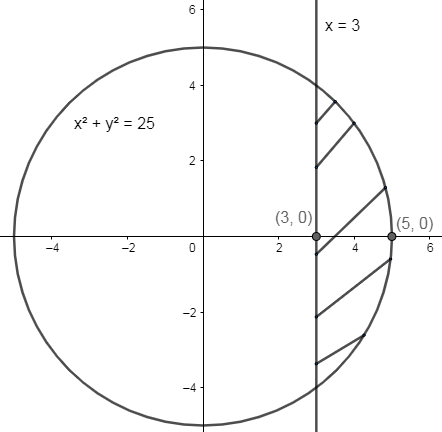
As we see, the shaded region in the above graph, we get the smaller area to be solved.
Therefore, we will find the area with respect to y, that is we will write the equation of a circle in terms of x and write the range of x, that is
The equation of a circle is ${{x}^{2}}+{{y}^{2}}=25$ ------ (2)
Now, we will subtract ${{x}^{2}}$ on both sides in equation (2), we get
${{x}^{2}}+{{y}^{2}}-{{x}^{2}}=25-{{x}^{2}}$
As we know, the same terms with opposite signs cancel out each other, thus we get
${{y}^{2}}=25-{{x}^{2}}$
Now, we will take the square root on both sides of the above equation, we get
$\sqrt{{{y}^{2}}}=\sqrt{25-{{x}^{2}}}$
On further solving, we get
$y=\sqrt{25-{{x}^{2}}}$ --------- (3)
Now, from the graph, we see that the line to cut the circle at $x=3$ , therefore, the minimum range for x is equal to 3.
Also, we see that the smaller part of the circle ends at x=5, therefore, the maximum range for x is equal to 5.
Thus, from equation (3), minimum, and maximum range of x, the definite integral is equal to
$\int_{3}^{5}{\sqrt{25-{{x}^{2}}}}dx$
Thus, we see from the graph that the line cut the circle into 2 equal parts, therefore the area of the smaller part is equal to
$Area=2\int_{3}^{5}{\sqrt{25-{{x}^{2}}}}dx$ which is our required solution.
Therefore, the smaller area cut of the equation of circle ${{x}^{2}}+{{y}^{2}}=25$ by the line $x=3$ is equal to $2\int_{3}^{5}{\sqrt{25-{{x}^{2}}}}dx$.

Note: While solving this problem, keep in mind the formula you are using. Do the step-by-step calculations to avoid an error. Draw the graph of a circle by using the standard form of the equation of circle ${{(x-h)}^{2}}+{{(y-k)}^{2}}={{r}^{2}}$ , where (h, k) is the center and r is the radius of the circle.