Question

How do you write in simplest radical form the coordinates of point $A$ if $A$ is on the terminal side of angle in standard position whose degree measure is $\theta :OA=15,\theta ={{135}^{\circ }}$ ?

Answer 1

Here in this question we have been asked to write the coordinates of point $A$ in simplest radical form if it is given that $A$ is on the terminal side of angle in standard position whose degree measure is $\theta :OA=15,\theta ={{135}^{\circ }}$ . For answering this question we will make a reference angle inside a circle of radius $15$ and a triangle inside it.

Complete step-by-step solution:
Now considering from the question we have been asked to write the coordinates of point $A$ in simplest radical form if it is given that $A$ is on the terminal side of angle in standard position whose degree measure is $\theta :OA=15,\theta ={{135}^{\circ }}$ .
For answering this question we will make a reference angle inside a circle of radius $15$ and a triangle inside it.
The reference image will look like:

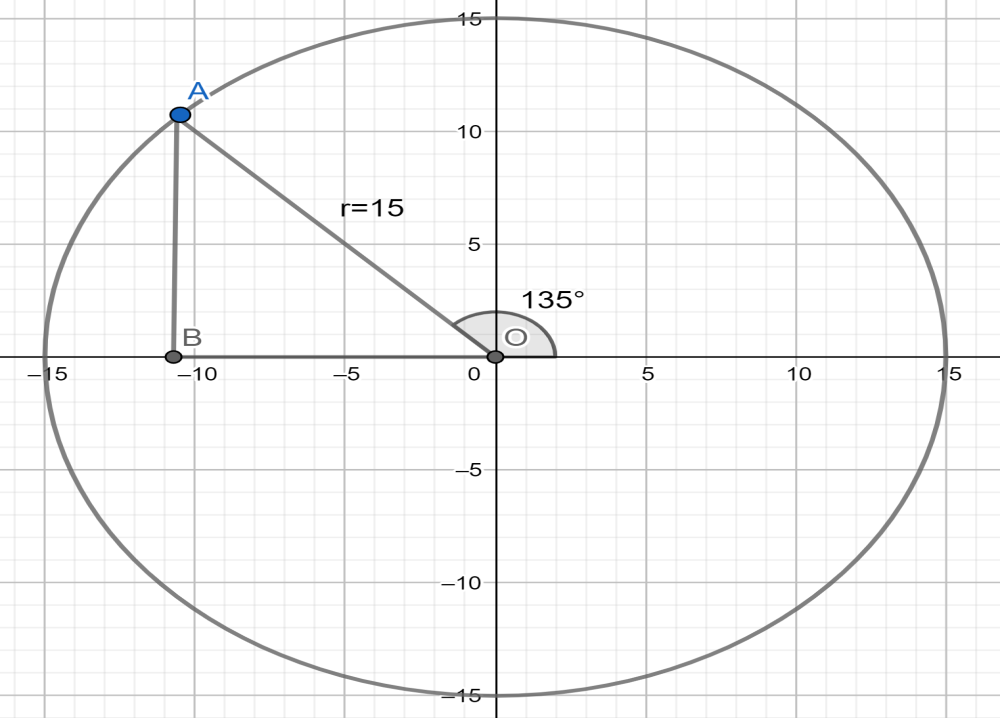
Now we can say that the inner angle of the triangle will be given as $\angle AOB={{180}^{\circ }}-{{135}^{\circ }}={{45}^{\circ }}$ .
Since we know that the coordinates of point $A$ will be given as $\left( -OB,AB \right)$ because $OB$ is the distance on the x-axis and it lies on the negative side of x-axis and $AB$ is the distance on the y-axis.
Since the reference triangle is right angle we can say that the other angle is also ${{45}^{\circ }}$ as the sum of all the angles in a triangle is ${{180}^{\circ }}$ .
As we had assumed the radius of the circle to be $15$ we will be having $OA=15$ the length of the hypotenuse.
Since two angles are equal the sides corresponding to those angles will also be equal let us assume them to be $x$ .
From the Pythagoras theorem, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
Here it will be mathematically given as ${{15}^{2}}={{x}^{2}}+{{x}^{2}}$ .
By simplifying this we will have
$\begin{aligned} & 225=2{{x}^{2}} \\\ & \Rightarrow x=\sqrt{\dfrac{225}{2}} \\\ & \Rightarrow x=\dfrac{15}{\sqrt{2}}\Rightarrow OB=AB \\\ \end{aligned}$ .
Therefore we can conclude that the coordinates of $A$ in the simplest radical form when it is given that $A$ is on the terminal side of angle in standard position whose degree measure is $\theta :OA=15,\theta ={{135}^{\circ }}$ can be written as $\left( \dfrac{-15}{\sqrt{2}},\dfrac{15}{\sqrt{2}} \right)$ .

Note: While answering questions of this type we should be sure with the circular concepts that we are going to apply in the process and the calculations that we are going to perform in between. We should not forget to consider that the point lies in the second quadrant if we missed it then we will have the answer as $\left( \dfrac{15}{\sqrt{2}},\dfrac{15}{\sqrt{2}} \right)$ .