Question

How do you write $F\left( x \right) = {x^2} - 2x + 5$ in vertex form?

Answer 1

We have to rewrite the given equation in vertex form. For this, complete the square for ${x^2} - 2x + 5$ and use the form $a{x^2} + bx + c$, to find the values of $a$, $b$, and $c$. Consider the vertex form of a parabola, $a{\left( {x + d} \right)^2} + e$. Next, substitute the values of $a$ and $b$ into the formula $d = \dfrac{b}{{2a}}$ and simplify the right side. Next, find the value of $e$ using the formula $e = c - \dfrac{{{b^2}}}{{4a}}$. Next, substitute the values of $a$, $d$, and $e$ into the vertex form $a{\left( {x + d} \right)^2} + e$. Next, set $y$ equal to the new right side and get the required vector form.

Formula used:
Vertex form of a parabola: $a{\left( {x + d} \right)^2} + e$
$d = \dfrac{b}{{2a}}$
$e = c - \dfrac{{{b^2}}}{{4a}}$
Vertex form: $y = a{\left( {x - h} \right)^2} + k$
Vertex: $\left( {h,k} \right)$
$p = \dfrac{1}{{4a}}$
Focus: $\left( {h,k + p} \right)$
Directrix: $y = k - p$

Complete step by step solution:
We have to rewrite the given function in vertex form.
For this, complete the square for ${x^2} - 2x + 5$.
Use the form $a{x^2} + bx + c$, to find the values of $a$, $b$, and $c$.
$a = 1,b = - 2,c = 5$
Consider the vertex form of a parabola.
$a{\left( {x + d} \right)^2} + e$
Now, substitute the values of $a$ and $b$ into the formula $d = \dfrac{b}{{2a}}$.
$d = \dfrac{{ - 2}}{{2 \times 1}}$
Simplify the right side.
$\Rightarrow d = - 1$
Find the value of $e$ using the formula $e = c - \dfrac{{{b^2}}}{{4a}}$.
$e = 5 - \dfrac{{{{\left( { - 2} \right)}^2}}}{{4 \times 1}}$
$\Rightarrow e = 4$
Now, substitute the values of $a$, $d$, and $e$ into the vertex form $a{\left( {x + d} \right)^2} + e$.
${\left( {x - 1} \right)^2} + 4$
Set $y$ equal to the new right side.
$y = {\left( {x - 1} \right)^2} + 4$
Which is the required vertex form.

$y = {\left( {x - 1} \right)^2} + 4$ is the vertex form of a given function.

Note: Vertex form of the quadratic function:
$y = a{\left( {x - h} \right)^2} + k$ where $\left( {h,k} \right)$ is the vertex or the “center” of the quadratic function or the parabola.
We can also find the vertex form of a given function by plotting the function and determining the vertex, $\left( {h,k} \right)$ of the given function.

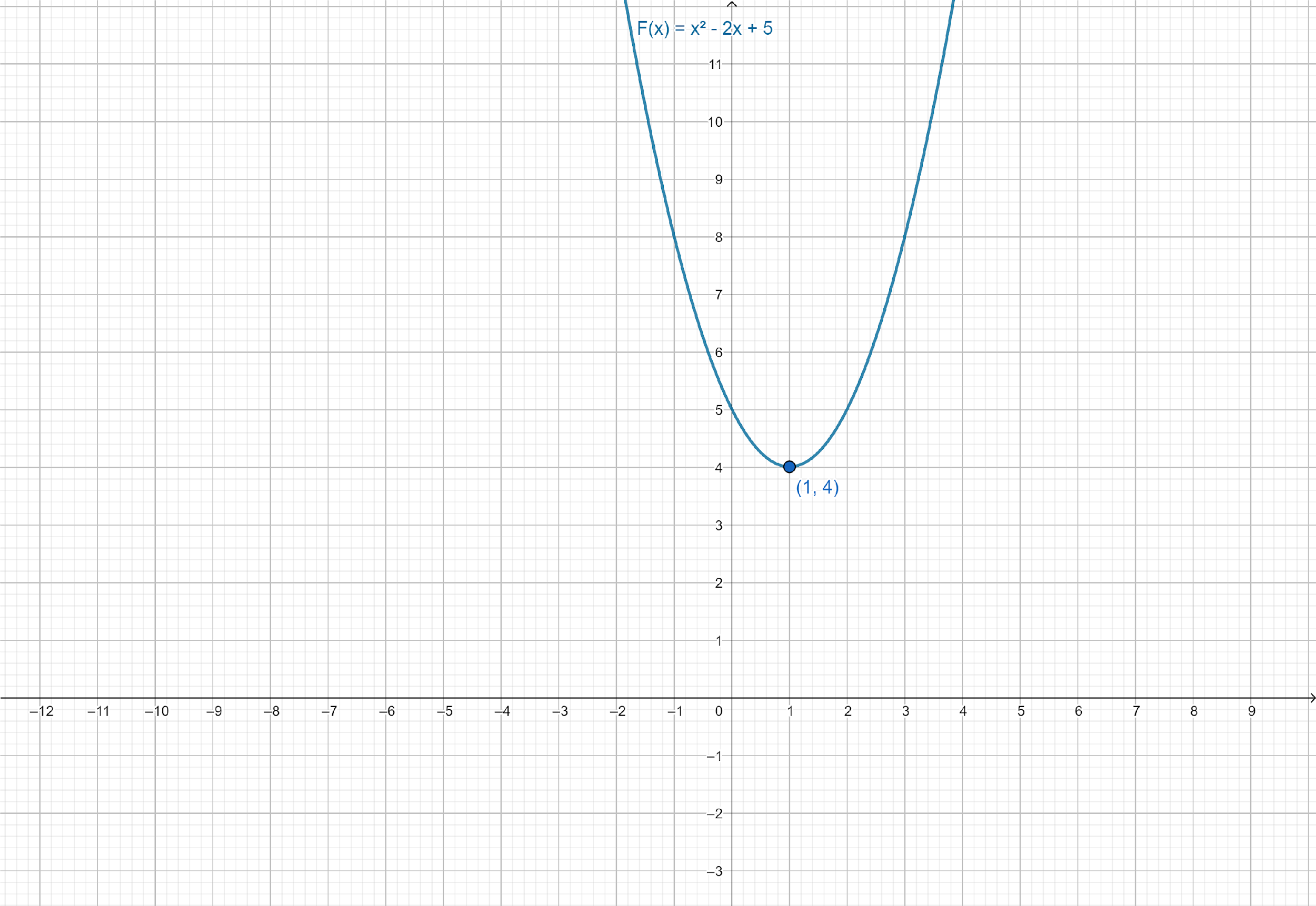
From the graph, we can observe that $\left( {1,4} \right)$ is the vertex of the parabola.
Put the value of $a,h,k$ in $y = a{\left( {x - h} \right)^2} + k$.
$y = {\left( {x - 1} \right)^2} + 4$ (As $a = 1$)