Question

How do you write equation of the line that passes through point $\left( {4,2} \right)$ and $\left( {6,6} \right)$

Answer 1

Hint : In order to determine the required equation of line, first find out the value of slope $m = \dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}$ by considering $\left( {4,2} \right)$ as$\left( {{x_1},{y_1}} \right)$and $\left( {6,6} \right)$ as$\left( {{x_2},{y_2}} \right)$.Now put the slope $m$ and any point in the slope point form $\left( {y - {y_1}} \right) = m\left( {x - {x_1}} \right)$ and simplify it to obtain the required equation.

Complete step-by-step answer :
We are given two points as $\left( {4,2} \right)$ and $\left( {6,6} \right)$ .
In this question we are supposed to find out the equation of line which is passing through the points $\left( {4,2} \right)$ and $\left( {6,6} \right)$ .
For this we have to first determine the slope of the line passing through these two points. So, as we know the slope between two points is given by $m = \dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}$ where$\left( {{x_1},{y_1}} \right)$and $\left( {{x_2},{y_2}} \right)$are the coordinates of two points.
Considering $\left( {4,2} \right)$ as$\left( {{x_1},{y_1}} \right)$and $\left( {6,6} \right)$ as$\left( {{x_2},{y_2}} \right)$, we have the value of slope as
$m = \dfrac{{6 - 2}}{{6 - 4}} \\\ m = \dfrac{4}{2} \\\ m = 2 \;$
Thus we get the slope $m$ equals $2$ .
The Point-Slope Formula of straight line is
$\left( {y - {y_1}} \right) = m\left( {x - {x_1}} \right)$ where $\left( {{x_1},{y_1}} \right)$ is the point on the line .
So, we have the slope of the required line as $m = 2$ and also it is passing through the point $\left( {4,2} \right)$ .We can write the equation of straight line using the point slope form as
$\Rightarrow \left( {y - 2} \right) = 2\left( {x - 4} \right)$
Expanding the bracket on RHS, we get
$\Rightarrow y - 2 = 2x - 8$
combining all the like terms and rewrite the equation into the general equation form as $y = mx + c$ , we can obtain the above equation as

$$\Rightarrow y = 2x - 8 + 2 \\\ \Rightarrow y = 2x - 6 \;$$

Therefore, the equation of line passing through the points $\left( {4,2} \right)$ and $\left( {6,6} \right)$ is equal to $y = 2x - 6$.
So, the correct answer is “ $y = 2x - 6$”.

Note : 1. The graph of the equation of line$y = 2x - 6$ is shown below.

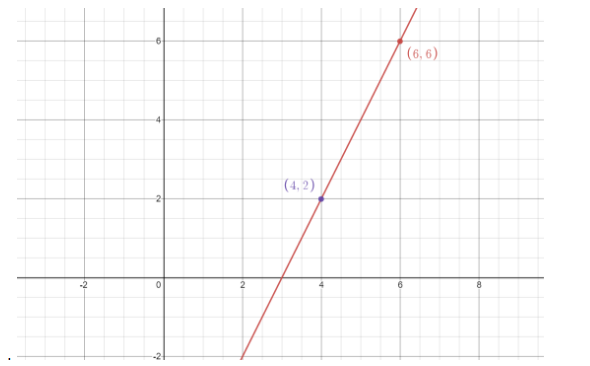
You can verify the result as both the points are lying on the straight line.
2.Slope of line perpendicular to the line having slope $m$ is equal to $- \dfrac{1}{m}$ .
3.We should have a better knowledge in the topic of geometry to solve this type of question easily. We should know the Point-slope form $\left( {y - {y_1}} \right) = m\left( {x - {x_1}} \right)$ where $\left( {{x_1},{y_1}} \right)$ is the point on the line $m$ as the form and also the Slope-intercept form of line as $y = mx + c$ where $m$ is the slope of the line.
4. The general equation for lines parallel to $y = 2x - 6$will be $y = 2x \pm k$where $k$ can be any integer.
5. Write the coordinates with proper signs while determining the slope and equation.
6. In the point slope form we have taken $\left( {4,2} \right)$ . You can also take $\left( {6,6} \right)$ .