Question

How do you write an equation that passes through the origin and has a slope of 3 ?

Answer 1

From the question given a line passing through the origin and has a slope of $3$, we have to find the equation of that line. As we know that the line passing through the origin means the line passing through the point $\left( 0,0 \right)$. And in the question the slope “m” is equal to $3$. As we know that if any line has a slope “m” and it is passing through the point $\left( {{x}_{1}},{{y}_{1}} \right)$, then the line equation is $y-{{y}_{1}}=m\left( x-{{x}_{1}} \right)$. By this we will get the required line equation.

Complete step-by-step solution:
From the question given a line passing through the origin, it means the line passing through the point
$\Rightarrow \left( 0,0 \right)$
As mentioned in the question that the line has a slope of 3, that is the value of “m” is,
$\Rightarrow m=3$
As we know that if any line has a slope “m” and it is passing through the point $\left( {{x}_{1}},{{y}_{1}} \right)$, then the line equation is
$\Rightarrow y-{{y}_{1}}=m\left( x-{{x}_{1}} \right)$
By comparing here, we will get,
$\Rightarrow m=3$
$\Rightarrow \left( {{x}_{1}},{{y}_{1}} \right)=\left( 0,0 \right)$
By substituting the above values in their respective positions, we will get the equation of line,
$\Rightarrow y-\left( 0 \right)=3\left( x-0 \right)$
By simplifying further, we will get,
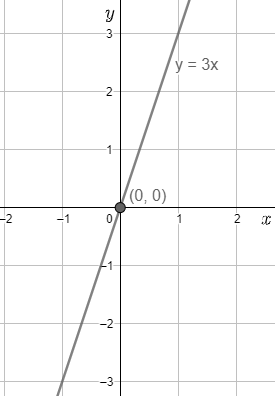
$\Rightarrow y=3x$
$\Rightarrow 3x-y=0$
Therefore, this is the required line equation which is passing through the origin and has a slope of $3$ .

Note: Students should know the basic formulas of coordinate geometry, students should know the various general forms of the line equation, like
$\begin{aligned} & \Rightarrow y=mx+c \\\ & \Rightarrow y-{{y}_{1}}=m\left( x-{{x}_{1}} \right) \\\ & \Rightarrow y-{{y}_{1}}=\dfrac{\left( {{y}_{2}}-{{y}_{1}} \right)}{\left( {{x}_{2}}-{{x}_{1}} \right)}\left( x-{{x}_{1}} \right) \\\ \end{aligned}$
According to the given information in the question we have to use the respective line equation.