Question

How do you write an equation of the sine function with amplitude $5$, period $3pi$, and phase shift $-pi$?

Answer 1

From the question we are given the amplitude, period and phase shift and we are asked to find the equation of the sine function. For solving this question we will use the general form of sine function with amplitude, period and phase shift given. The general form of sine is $\Rightarrow y=a\sin b\left( x-p.s \right)$. We will also use the basic mathematical operations like addition, multiplication etc.. and simplify the equation and find the required solution. So, we proceed with our solution as follows.

Complete step-by-step solution:
Firstly, the general form of sine function with amplitude, period and phase shift parameters is as follows.
$\Rightarrow y=a\sin b\left( x-p.s \right)$
Here in the above general form the amplitude is $a$ and the phase shift is P.S. The parameter $b$ is $\dfrac{2\pi }{period}$.
So, from the given question we know that the amplitude, phase shift and $b$ will be as follows.
$\Rightarrow a=5$
$\Rightarrow p.s=-\pi$
The parameter $b$ in the general form for our question will be as follows.
$\Rightarrow b=\dfrac{2\pi }{period}$
$\Rightarrow b=\dfrac{2\pi }{3\pi }$
$\Rightarrow b=\dfrac{2}{3}$
So, now we will use the substitution method and substitute the value we got in the general form and find the sine function.
$\Rightarrow y=a\sin b\left( x-p.s \right)$
$\Rightarrow y=5\sin \dfrac{2}{3}\left( x-(-\pi ) \right)$
Now, we expand the brackets by using multiplication operations.
$\Rightarrow y=5\sin \dfrac{2}{3}\left( x+\pi \right)$
The graph of the function will be as follows.

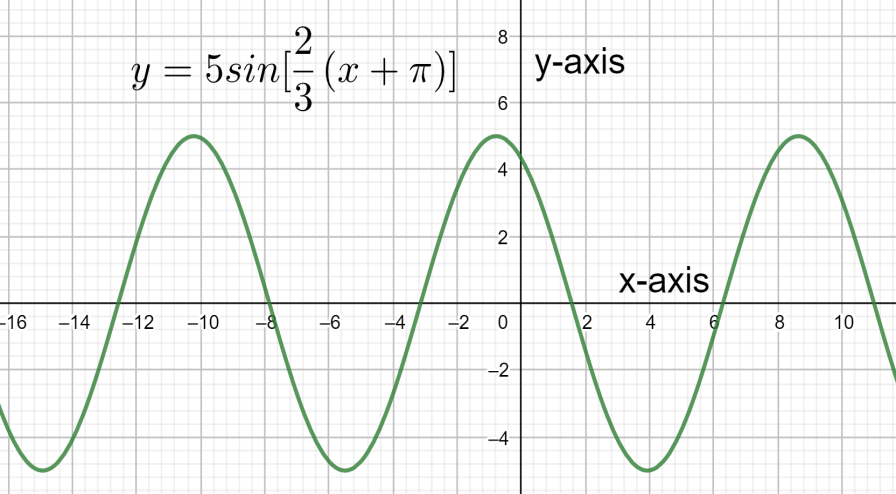
Note: Students must be very careful in doing the calculations. Students must have good knowledge in the concept of trigonometric functions and their forms. Students should know the general form of sine function with parameters of amplitude, phase shift and period which is as follows.
$\Rightarrow y=a\sin b\left( x-p.s \right)$