Question

How do you write an equation of the line with $\left( 8,3 \right)$, $m=6$?

Answer 1

From the question given a line passing through the point $\left( 8,3 \right)$ and has a slope of $m=6$, we have to find the equation of that line. As we know that if any line has a slope “m” and it is passing through the point $\left( {{x}_{1}},{{y}_{1}} \right)$, then the line equation is $y-{{y}_{1}}=m\left( x-{{x}_{1}} \right)$. By this we will get the required line equation.

Complete step-by-step solution:
From the question given the line passing through the point
$\Rightarrow \left( 8,3 \right)$
As mentioned in the question that the line has a slope of, that is the value of “m” is,
$\Rightarrow m=6$
As we know that if any line has a slope “m” and it is passing through the point $\left( {{x}_{1}},{{y}_{1}} \right)$, then the line equation is
$\Rightarrow y-{{y}_{1}}=m\left( x-{{x}_{1}} \right)$
By comparing here, we will get,
$\Rightarrow m=6$
$\Rightarrow \left( {{x}_{1}},{{y}_{1}} \right)=\left( 8,3 \right)$
By substituting the above values in their respective positions, we will get the equation of line,
$\Rightarrow y-\left( 3 \right)=6\left( x-8 \right)$
By simplifying further, we will get,
$\Rightarrow y-3=6x-48$
By simplifying further, we will get,
$\Rightarrow y=6x-45$
By simplifying further, we will get,
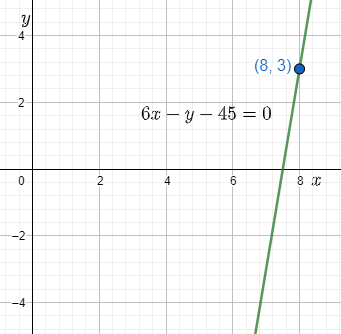
$\Rightarrow 6x-y-45=0$
Therefore, this is the required line equation which is passing through the point $\left( 8,3 \right)$ and has a slope of $m=6$.
The figure will be as follows.

Note: Students should know the basic formulas of coordinate geometry, students should know the various general forms of the line equation, like
Slope intercept form
$\Rightarrow y=mx+c$
Point slope form
$\Rightarrow y-{{y}_{1}}=m\left( x-{{x}_{1}} \right)$
By further expanding the point slope form
$\Rightarrow y-{{y}_{1}}=\dfrac{\left( {{y}_{2}}-{{y}_{1}} \right)}{\left( {{x}_{2}}-{{x}_{1}} \right)}\left( x-{{x}_{1}} \right)$
According to the given information in the question we have to use the respective line equation.