Question

How do you write an equation of an ellipse in standard form given foci are $\left( -2,1 \right)$ and $\left( -2,5 \right)$ and vertices are $\left( -2,-1 \right)$ and $\left( -2,7 \right)$?

Answer 1

From the given question we have been asked to find the equation of an ellipse in the standard form with foci and vertices given. For solving this question first we will find the centre of the ellipse as we can see the abscissas of vertices being the same and after finding the centre of the ellipse we will use the general form of ellipse which is $\Rightarrow \dfrac{{{\left( x-x' \right)}^{2}}}{{{b}^{2}}}+\dfrac{{{\left( y-y' \right)}^{2}}}{{{a}^{2}}}=1$ and solve the question.

Complete step-by-step solution:
Given that the coordinate of vertices of the ellipse are $\left( -2,-1 \right)$ and $\left( -2,7 \right)$.
We can see that the abscissas of the vertices that is the x coordinate is being the same and the axis of the ellipse is parallel to the y-axis.
So, the major part is parallel to y-axis. The centre will be as follows.
$~\Rightarrow \left( \dfrac{-2-2}{2},\dfrac{-1+7}{2} \right)$
$~\Rightarrow \left( -2,3 \right)$
If a and b are halves of the major and minor axis respectively then the standard equation of ellipse may be written as following.
$\Rightarrow \dfrac{{{\left( x-x' \right)}^{2}}}{{{b}^{2}}}+\dfrac{{{\left( y-y' \right)}^{2}}}{{{a}^{2}}}=1$
Now we are to find out a and b.
Again it is also given the coordinate of foci which are $\left( -2,1 \right)$ and $\left( -2,5 \right)$.
Now a is the distance between centre and vertex.
$~\Rightarrow a=\sqrt{{{\left( -2+2 \right)}^{2}}+{{\left( 7-3 \right)}^{2}}}=4$
Now if e represents the eccentricity of the ellipse then
$\Rightarrow e=\sqrt{\dfrac{{{a}^{2}}-{{b}^{2}}}{{{a}^{2}}}}$
Now the distance between centre and focus is $ae$.
$\Rightarrow ae=\sqrt{{{\left( -2+2 \right)}^{2}}+{{\left( 3-5 \right)}^{2}}}=2$
$\Rightarrow {{a}^{2}}{{e}^{2}}=\dfrac{{{a}^{2}}\left( {{a}^{2}}-{{b}^{2}} \right)}{{{a}^{2}}}={{2}^{2}}$
$\Rightarrow {{4}^{2}}-{{b}^{2}}={{2}^{2}}$
$\Rightarrow {{b}^{2}}=12$
Now we insert the values of a and b in the standard equation.
We get the equation as follows.
$\Rightarrow \dfrac{{{\left( x+2 \right)}^{2}}}{12}+\dfrac{{{\left( y-3 \right)}^{2}}}{16}=1$
The graph will be as follows.

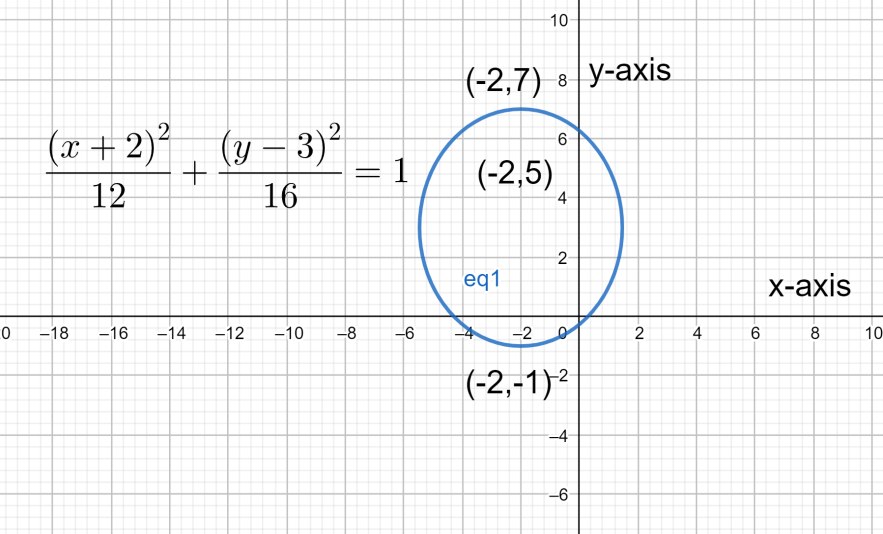
Note: Students should be very careful in doing the calculations. Students should have good knowledge in the concept of ellipse and its properties. Students should know formulae in ellipse such as,
$\Rightarrow e=\sqrt{\dfrac{{{a}^{2}}-{{b}^{2}}}{{{a}^{2}}}}$
$\Rightarrow \dfrac{{{\left( x-x' \right)}^{2}}}{{{b}^{2}}}+\dfrac{{{\left( y-y' \right)}^{2}}}{{{a}^{2}}}=1$.