Question

How do you write an equation of an ellipse given endpoints of major axis at $\left( -11,5 \right)$ and $\left( 7,5 \right)$ and endpoints of the minor axis at $\left( -2,9 \right)$ and $\left( -2,1 \right)$?

Answer 1

In this question we have been given with the endpoints of the major axis and the minor axis of an ellipse. We will use the general form of the endpoints of the major axis which is in the form $\left( h-a,k \right)$ and $\left( h+a,k \right)$, and the general form of the endpoint of the major axis which is the form $\left( h,k-b \right)$ and $\left( h,k+b \right)$. We will get equations and then solve for the value of $a$ and $b$, and write the equation of the ellipse in the standard form as $\dfrac{{{\left( x-h \right)}^{2}}}{{{a}^{2}}}+\dfrac{{{\left( y-k \right)}^{2}}}{{{b}^{2}}}=1$.

Complete step-by-step solution:
We have the endpoints of the major axis as:
$\left( -11,5 \right)$ and $\left( 7,5 \right)$
The general form of the endpoints is:
$\left( h-a,k \right)$ and $\left( h+a,k \right)$
Therefore, we can write:
$k=5\to \left( 1 \right)$
$h-a=-11\to \left( 2 \right)$
$h+a=7\to \left( 3 \right)$
We have the endpoints of the minor axis as:
$\left( -2,9 \right)$ and $\left( -2,1 \right)$
The general form of the endpoints is:
$\left( h,k-b \right)$ and $\left( h,k+b \right)$
Therefore, we can write:
$h=-2\to \left( 4 \right)$
$k-b=1\to \left( 5 \right)$
$k+b=9\to \left( 6 \right)$
Subtracting $\left( 2 \right)$ from $\left( 3 \right)$, we get:
$\Rightarrow 2a=18$
On dividing both the sides of the expression by $2$, we get:
$\Rightarrow a=9$
Subtracting $\left( 5 \right)$ from $\left( 6 \right)$, we get:
$\Rightarrow 2b=8$
On dividing both the sides of the expression by $2$, we get:
$\Rightarrow b=4$
Now we know the general form of the equation of an ellipse is $\dfrac{{{\left( x-h \right)}^{2}}}{{{a}^{2}}}+\dfrac{{{\left( y-k \right)}^{2}}}{{{b}^{2}}}=1$.
On substituting the values of $h,k,a$ and $b$, we get:
$\dfrac{{{\left( x-\left( -2 \right) \right)}^{2}}}{{{9}^{2}}}+\dfrac{{{\left( y-5 \right)}^{2}}}{{{4}^{2}}}=1$, which is the required solution.
Drawing the ellipse on the graph, we get:

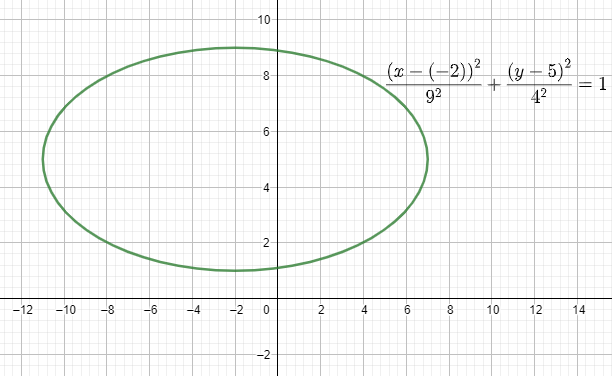
Note: The major axis of the ellipse represents the axis which is longer, in this case the $x$ axis and the minor axis represents the axis which is smaller, in this case the $y$ axis. $a$ represents the major axis and $b$ represents the minor axis. It is to be noted that in this case we have with us a horizontal ellipse since $a>b$. If $b>a$ then the ellipse formed is called a vertical ellipse.