Question

How do you write an equation of a line passing through (0,2), perpendicular to $y=4x-3$ ?

Answer 1

We will use $y=mx+b$ first to find the value of the slope of the equation$y=4x-3$ . We will then use the formula ${{m}_{p}}=-\dfrac{1}{m}$ , to find the slope of a perpendicular line. By substituting the values in the point-slope formula, $\left( y-{{y}_{1}} \right)=m\left( x-{{x}_{1}} \right)$ , we will get the required equation.

Complete step by step answer:
We are given a point (0, 2), and an equation $y=4x-3$ . We know that $y=4x-3$ is of the form $y=mx+b$ , where m is the slope of the line b is the y-intercept.
Now, let us compare the equation $y=4x-3$ with the standard slope equation, $y=mx+b$ . We will get
$m=4\text{ and }b=-3$ .
Let us denote the slope of the perpendicular as ${{m}_{p}}$ .
We know that the slope of a perpendicular line is given by
${{m}_{p}}=-\dfrac{1}{m}$ .
Let us now substitute the values.
$\Rightarrow {{m}_{p}}=-\dfrac{1}{4}$
We will now use a point-slope formula to find the equation of the required line. We know that the point-slope formula is given as
$\left( y-{{y}_{1}} \right)=m\left( x-{{x}_{1}} \right)$ , where m is the slope and $\left( {{x}_{1}},{{y}_{1}} \right)$ denotes the point through which the line passes.
Now, we have to substitute the values in the above formula. Here, the slope is ${{m}_{p}}$ and the point is (0,2) . We will get
$\left( y-2 \right)=-\dfrac{1}{4}\left( x-0 \right)$
$\Rightarrow \left( y-2 \right)=-\dfrac{1}{4}x$
Let us take 2 from LHS to RHS. We will get
$y=-\dfrac{1}{4}x+2$

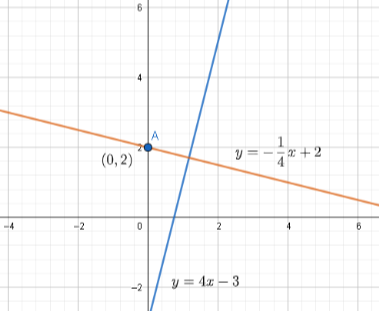
Hence, the required equation of the line is $y=-\dfrac{1}{4}x+2$.

Note: There are chances for students to make mistakes and they must refrain from committing them. They may consider the slope from the formula $y=mx+b$ as b instead of m. They may write the point-slope formula as $\left( x-{{x}_{1}} \right)=m\left( y-{{y}_{1}} \right)$ instead of $\left( y-{{y}_{1}} \right)=m\left( x-{{x}_{1}} \right)$ . In the point-slope formula, you may substitute the value of m instead of ${{m}_{p}}$ .