Question

How do you write an equation of a line parallel to the graph of $2x+5y=3$ and the x-intercept is -2?

Answer 1

We will convert $2x+5y=3$ in the form $y=mx+b$ and find the slope. Since parallel lines will have the same slope, the slope of the required line will also be the same. Now, we have to find the y-intercept of the required line. We know that the x-intercept will occur when $y=0$ . By substituting the values of y, m and x in the equation $y=mx+b$ , we will get the value of b. Now, substituting the value of m and b in $y=mx+b$ to get the equation of the required line.

Complete step by step answer:
We are given an equation $2x+5y=3$ . Let us make this in the form $y=mx+b$ , where m is the slope of the line b is the y-intercept. Let us make the y terms on LHS and the remaining on the RHS.
$\Rightarrow 5y=-2x+3$
Now, we have to take the 5 from LHS to RHS.
$\begin{aligned} & \Rightarrow y=\dfrac{-2x+3}{5} \\\ & \Rightarrow y=\dfrac{-2}{5}x+\dfrac{3}{5} \\\ \end{aligned}$
Let us now compare the above equation with standard slope equation, $y=mx+b$ . We will get
$m=\dfrac{-2}{5}\text{ and }b=\dfrac{3}{5}$ .
We know that parallel line will have the same slope. Hence the slope of the required line will be $m=\dfrac{-2}{5}\text{ }$ .
We are given that the x-intercept of the required line is -2. This means that at x-intercept, $y=0$ .
Now, let us find the y-intercept of the required line by using the formula $y=mx+b$ by substituting $y=0,x=-2$ and $m=\dfrac{-2}{5}\text{ }$ in it.
$\begin{aligned} & \Rightarrow 0=\dfrac{-2}{5}\text{ }\left( -2 \right)+b \\\ & \Rightarrow 0=\dfrac{4}{5}+b \\\ & \Rightarrow b=-\dfrac{4}{5} \\\ \end{aligned}$
Now, let us substitute the values, $m=\dfrac{-2}{5}\text{ }$ and $b=-\dfrac{4}{5}$ in $y=mx+b$ to get the equation of the required line.
$\Rightarrow y=-\dfrac{2}{5}\text{ }x-\dfrac{4}{5}\text{ }$

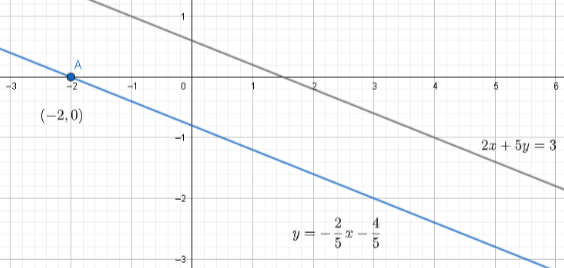
Hence, the required equation of the line is $y=-\dfrac{2}{5}\text{ }x-\dfrac{4}{5}\text{ }$ .

Note: Students may commit mistake by thinking that parallel lines will have the slope in the form ${{m}_{p}}=-\dfrac{1}{m}$ which is the slope of the perpendicular line. Note that at x-intercept $y=0$ and at y-intercept x will be 0. In $y=mx+b$ ,students may misunderstand b as the slope and m as the x-intercept.