Question

How do you write an equation of a line given $\left( 0,4 \right)$ and is parallel to $y=3x-7$?

Answer 1

First we will find the slope of the line as the lines are parallel to each other so both have the same slope. Then by using the slope-intercept form we will calculate the y-intercept by substituting the value of the given point. Then by using the values obtained we get the desired answer.

Complete step by step answer:
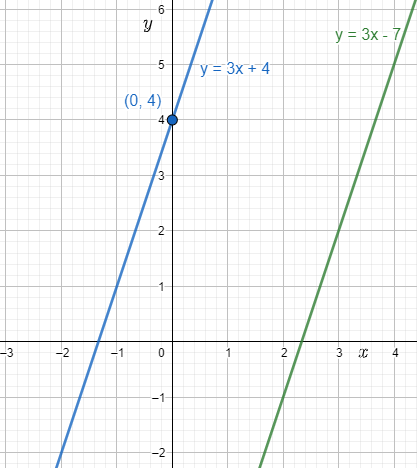
We have been given that a line is going through $\left( 0,4 \right)$ and parallel to $y=3x-7$.
We have to find the equation of the line.
Now, we know that the slope intercept form of a line is given as $y=mx+c$, where m is the slope of line and c is the y-intercept of the line.
Now, we have given the equation of another line which is $y=3x-7$.
Now, comparing the equation with the general equation we will get
$\Rightarrow m=3,y=-7$
Now, both the lines are parallel it means they have same slope so the slope of the line will be $m=3$
Now, the general equation of the line will be
$\Rightarrow y=3x+c$
Now, the line is going through the point $\left( 0,4 \right)$.
So let us substitute $x=0$ and $y=4$ in the above equation then we will get
$\Rightarrow 4=3\times 0+c$
Now, simplifying the above obtained equation we will get
$\begin{aligned} & \Rightarrow 4=0+c \\\ & \Rightarrow c=4 \\\ \end{aligned}$
So the equation of the line with slope 3 and y-intercept 4 will be
$y=3x+4$
Hence above is the required equation of line.

Note: The point to be noted is that while calculating the slope of the line the coefficient of y must be 1. Also the equation of the line must be in general form $y=mx+c$ while calculating the slope and y-intercept of the line.