Solveeit Logo
Login

Question

Question: How do you write an equation of a circle with centre \[\left( -2,1 \right)\] and the radius with end...

How do you write an equation of a circle with centre (−2,1)\left( -2,1 \right) and the radius with endpoint at (1,0)\left( 1,0 \right).

Explanation

Solution

In this problem, we have to find the equation of the circle. We know that the general equation of the circle is (x−h)2+(y−k)2=r2{{\left( x-h \right)}^{2}}+{{\left( y-k \right)}^{2}}={{r}^{2}} . We are given the centre (−2,1)\left( -2,1 \right), we have to find the radius, r. we can find the distance between the centre and the radius using the distance formula to find the value of r, we can then substitute the r value and the given centre to find the equation of the given circle.

Complete step by step solution:
We know that the general equation of the circle is,
(x−h)2+(y−k)2=r2{{\left( x-h \right)}^{2}}+{{\left( y-k \right)}^{2}}={{r}^{2}}
Where, (h,k)\left( h,k \right) is the centre and r is the radius.
We are given the centre, (h,k)\left( h,k \right) is (−2,1)\left( -2,1 \right).
We can now find the value of the radius using the distance formula.
We know that the distance between the centre and the radius is,
⇒r=(x2−x1)2+(y2−y1)2\Rightarrow r=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}
We can now substitute the centre (−2,1)\left( -2,1 \right) and the endpoint (1,0)\left( 1,0 \right), we gwt
⇒r=(−2−1)2+(1−0)2=10\Rightarrow r=\sqrt{{{\left( -2-1 \right)}^{2}}+{{\left( 1-0 \right)}^{2}}}=\sqrt{10}
The value of r = 10.
We can now substitute the value of r and the centre point in the general equation of the circle, we get
⇒(x−(−2))2+(y−1)2=(10)2\Rightarrow {{\left( x-\left( -2 \right) \right)}^{2}}+{{\left( y-1 \right)}^{2}}={{\left( \sqrt{10} \right)}^{2}}
Now we can simplify the above step, we get
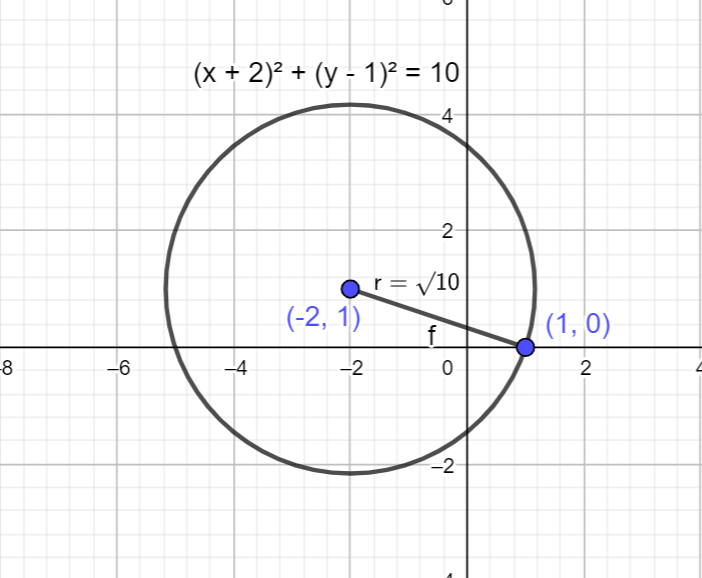
⇒(x+2)2+(y−1)2=10\Rightarrow {{\left( x+2 \right)}^{2}}+{{\left( y-1 \right)}^{2}}=10

Therefore, the equation of the circle is (x+2)2+(y−1)2=10{{\left( x+2 \right)}^{2}}+{{\left( y-1 \right)}^{2}}=10.

Note: Students make mistakes while finding the value of radius, we should know that we can obtain the radius value by distance formula, with the given centre point and the end point. We should also know the general equation of the circle formula with centre and radius, r, to find the equation of the circle.