Question

How do you write an equation in standard form when we are given points $\left( 3,3 \right)$ and $\left( 1,-3 \right)$?

Answer 1

In this problem we need to calculate the equation in standard form passing through the given points. We know that the standard equation of the line passing through the two points is given by $y=mx+c$ where $m$ is the slope of the equation and $c$ is the intercept value. To calculate the slope of the given equation we will use the formula $m=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}$ where $\left( {{x}_{1}},{{y}_{1}} \right)$, $\left( {{x}_{2}},{{y}_{2}} \right)$ are the points on the line. After calculating the value of $m$ we will substitute it in the standard equation. Now we need to calculate the value of $c$ for this we will substitute any one point in the calculated equation and simplify it to get the value of $c$. Now we will get the required equation by substituting all the values we have calculated.

Complete step-by-step solution:
Given points, $\left( 3,3 \right)$ and $\left( 1,-3 \right)$.
Comparing the above points with $\left( {{x}_{1}},{{y}_{1}} \right)$, $\left( {{x}_{2}},{{y}_{2}} \right)$, then we will get
${{x}_{1}}=3$, ${{y}_{1}}=3$, ${{x}_{2}}=1$, ${{y}_{2}}=-3$.
Now the slope of the equation can be calculated by
$m=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}$
Substituting the values, we have in the above equation, then we will have
$\begin{aligned} & \Rightarrow m=\dfrac{-3-3}{1-3} \\\ & \Rightarrow m=\dfrac{-6}{-2} \\\ & \Rightarrow m=3 \\\ \end{aligned}$
We know that the standard form of the equation of line is
$\Rightarrow y=mx+c$
Substituting $m=3$ in the above equation, then we will get
$\Rightarrow y=3x+c$
To find the value of $c$ we are going to substitute the point $\left( 3,3 \right)$ in the above equation, then we will have
$\begin{aligned} & \Rightarrow 3=3\left( 3 \right)+c \\\ & \Rightarrow 3=9+c \\\ & \Rightarrow c=-6 \\\ \end{aligned}$
Hence the equation of the line is given by
$\begin{aligned} & \Rightarrow y=3x-6 \\\ & \Rightarrow 3x-y-6=0 \\\ \end{aligned}$
Now the graph of the above equation will be

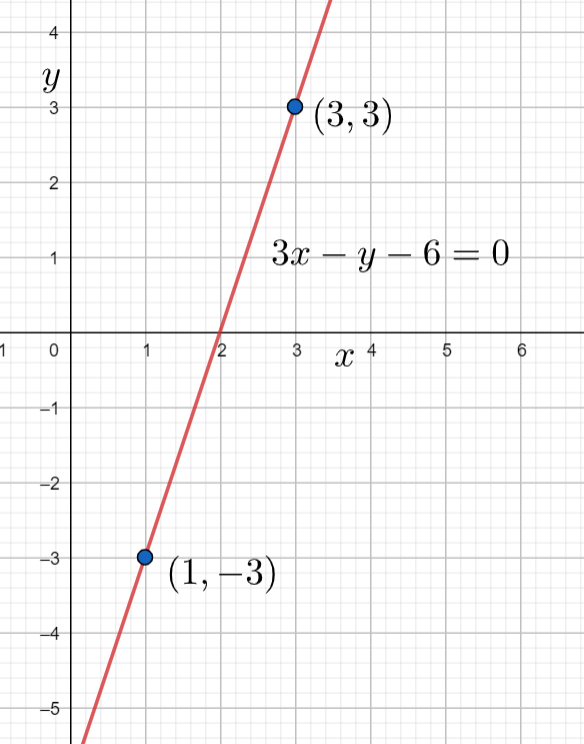
Note: We can also use another method to solve this problem. We can directly use the formula $y-{{y}_{1}}=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}\left( x-{{x}_{1}} \right)$. Substituting the all the values we have in the above equation, then we will get
$\begin{aligned} & \Rightarrow y-3=\dfrac{-3-3}{1-3}\left( x-3 \right) \\\ & \Rightarrow y-3=\dfrac{-6}{-2}\left( x-3 \right) \\\ & \Rightarrow y-3=3\left( x-3 \right) \\\ & \Rightarrow y-3=3x-9 \\\ & \Rightarrow y=3x-6 \\\ \end{aligned}$
From both the methods we got the same result.