Question

How do you write an equation in standard form given point $\left( 4,2 \right)$ and slope $-2$ ?

Answer 1

In order to find a solution to this problem, we will first have to analyze points that is $x$ and $y$coordinate from the given point and substitute in point-slope formula that is, $\left( y-{{y}_{1}} \right)=m\left( x-{{x}_{1}} \right)$.

Complete step-by-step solution:
We will start the solution by considering the given point as point $P\left( 4,2 \right)$.
Now we have our point $P$ that has two coordinates $x$ and $y$, so we have ${{x}_{1}}=4$ and ${{y}_{1}}=2$.
Now also we have our slope that is given in our problem that is $m=-2$.
Therefore, with this, we have all our requirements to write an equation in standard format.
We know standard form of equation as, $y=mx+c$ (where $m$ is the slope and $\left( x,y \right)$ is a point the line that passes through)
Hence, now we will substitute in the point-slope formula that is, $\left( y-{{y}_{1}} \right)=m\left( x-{{x}_{1}} \right)$.
So by substituting values, we get:
$\left( y-2 \right)=-2\left( x-4 \right)$
Now evaluating and simplifying above equation, we get:
$y-2=-2x+8$
Now transferring values from right hand side to left hand side and simplifying, we get:
$2x+y-2-8=0$
$2x+y-10=0$
Now by simplifying the equation into standard form that is, $y=mx+c$ we get:
$y=-2x+10$
Therefore, $y=-2x+10$ is the standard form of the equation of line.
We can represent this equation of line in graph form as:

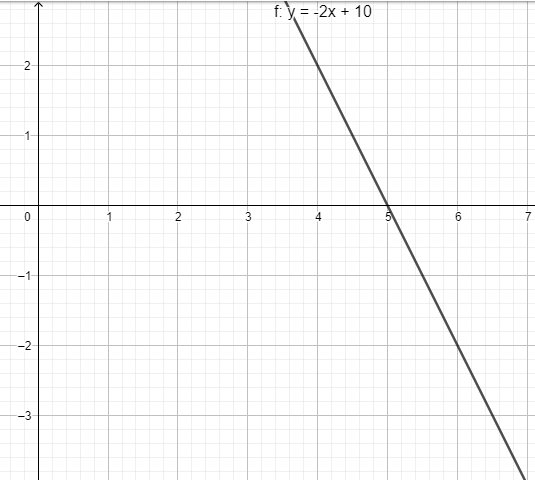
Note: The equation of a line can be found through various methods, some of the methods are Point-slope form, Slope-intercept form, Intercept form, Two-point form and depending on the available information we can write the equation of line.
After finding out the equation of line from one of the above methods, we have to write in a standard form that is, $y=mx+c$ , where $m$ is the slope and $\left( x,y \right)$ is a point that passes through the line.