Question

How do you write an equation in standard form for the horizontal and vertical line through $\left( 4,5 \right)$?

Answer 1

In this problem, we have to write an equation in standard form for the horizontal and vertical line through $\left( 4,5 \right)$. We can write the two equations for horizontal and the vertical line, from the standard form of a linear equation, we can substitute the points, in the standard form of the linear equation to find the both horizontal equation and the vertical equation.

Complete step by step answer:
We can now find the equation for a horizontal line through the point $\left( 4,5 \right)$.
In the above point, y = 5, where each and every value of x and y are 5.
We know that the standard form of a linear equation is,
$Ax+By=C$
Where, A, B, C are integers and A is a non-negative and A, B, C have no common factor other than one.
We can write it as,
$\Rightarrow 0x+1y=5$
Therefore, the equation of a horizontal line through the point $\left( 4,5 \right)$ is $y=5$.
We can now find the equation for a vertical line through the point $\left( 4,5 \right)$.
In the above point, x = 4, where each and every value of x and y are 4.
We know that the standard form of a linear equation is,
$Ax+By=C$
Where, A, B, C are integers and A is a non-negative and A, B, C have no common factor other than one.
We can write it as,
$\Rightarrow 1x+0y=4$
Therefore, the equation of a horizontal line through the point $\left( 4,5 \right)$ is $x=4$.

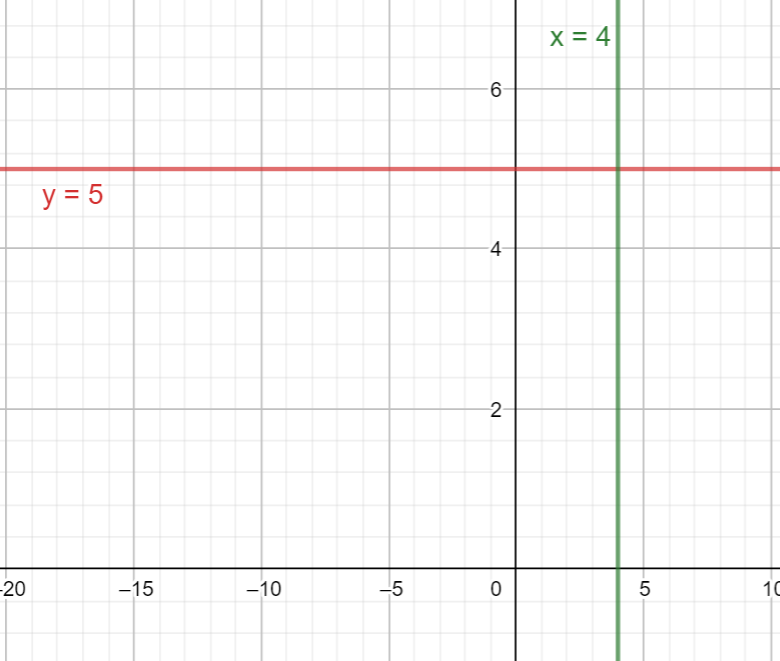
Note: We should always remember that, horizontal line goes left and right which is in the form of y=b, where b is the y-intercept, similarly vertical line goes up and down and is in the form of x=a, where a represents the shared x-coordinates of all points. Therefore, at the horizontal line, x=0 and at vertical line, y=0.