Question

How do you write an equation in slope intercept form given two points?

Answer 1

We first find the slope-intercept form for any point $P\left( x,y \right)$ and also find the equation of the line. In this case we actually take the help of the origin where $O\left( 0,0 \right)$. Then we take two arbitrary points and place them on the equation of the line and find the value of the slope and its equation.

Complete step-by-step solution:
We need to find the equation of the line which is inclined at a given angle with the positive direction of the axis of x and cuts off a given intercept from the axis of y.
Suppose the line $\overleftrightarrow{AB}$ intersects the X-axis at D and the y-axis at C. if the line makes an angle $\alpha$ with the positive direction of X-axis and $\overleftrightarrow{OC}=c$. We have to find the equation of the line $\overleftrightarrow{AB}$.

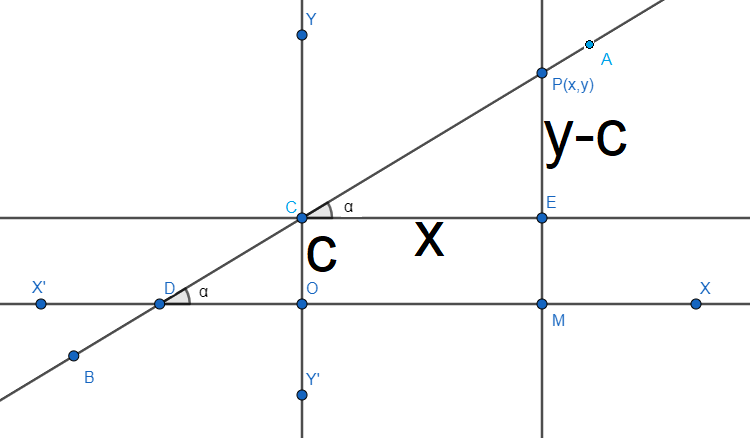
Let $P\left( x,y \right)$ be any point on the line $\overleftrightarrow{AB}$. We draw perpendicular $\overleftrightarrow{PM}$ on $\overleftrightarrow{OX}$ and $\overleftrightarrow{CE}$ perpendicular on $\overleftrightarrow{PM}$. Since, $CE||DM$, we have $\angle PCE=\angle CDM=\alpha$.
We also have $\overleftrightarrow{PM}=y;\overleftrightarrow{OC}=c;\overleftrightarrow{CE}=\overleftrightarrow{OM}=x$.
Then we have $\overleftrightarrow{PE}=\overleftrightarrow{PM}-\overleftrightarrow{EM}=\overleftrightarrow{PM}-\overleftrightarrow{OC}=y-c$.
Therefore, from the right-angled $\Delta PCE$, we get $\tan \alpha =\dfrac{\overleftrightarrow{PE}}{\overleftrightarrow{CE}}=\dfrac{y-c}{x}$.
We assume that the slope is m where $m=\tan \alpha$ which gives $m=\tan \alpha =\dfrac{y-c}{x}$.
The equation becomes $y=mx+c$.
Now if two points are given of the line where $P\left( x,y \right)$ and $Q\left( {{x}_{1}},{{y}_{1}} \right)$, the only change happens in the slope. For the above problem we took the second point as the origin.
Now both $P\left( x,y \right)$ and $Q\left( {{x}_{1}},{{y}_{1}} \right)$ goes through $y=mx+c$.
This gives $y=mx+c$ and ${{y}_{1}}=m{{x}_{1}}+c$. Subtracting we get $y-{{y}_{1}}=mx-m{{x}_{1}}=m\left( x-{{x}_{1}} \right)$.
The value of m becomes $m=\dfrac{\left( y-{{y}_{1}} \right)}{\left( x-{{x}_{1}} \right)}$. The equation becomes $\left( y-{{y}_{1}} \right)=m\left( x-{{x}_{1}} \right)$.

Note: We could have used the same process where we replace the origin value $O\left( 0,0 \right)$ with the point $Q\left( {{x}_{1}},{{y}_{1}} \right)$. The shifting of the origin will be sufficed to do that.