Question
Question: How do you write an equation in point slope form when the slope is \[\dfrac{1}{3}\] and the y-interc...
How do you write an equation in point slope form when the slope is 31 and the y-intercept is -4.
Solution
In this problem, we have to find an equation in point slope form. We are given a slope and y-intercept. We know that the equation of point slope form is (y−y1)=m(x−x1). Here we have to substitute the slope value and a point, where we have only slope. But we are given y-intercept, we know that at y-intercept the value of x is 0, therefore, we will get a point to be substituted in the formula to get an equation.
Complete step by step answer:
We know that the equation of point slope form is,
(y−y1)=m(x−x1)……. (1)
Where, m is the slope and (x,y) is the point.
We are given the slope, m = 31 and y-intercept, c = -4.
But here, we need a point to be substituted to get an equation.
We know that, at y-intercept the value of x is 0, i.e. x = 0.
Hence, we can get a point, (x,y)=(0,−4).
We can now substitute the above point and the slope value in the point slope formula (1), we get
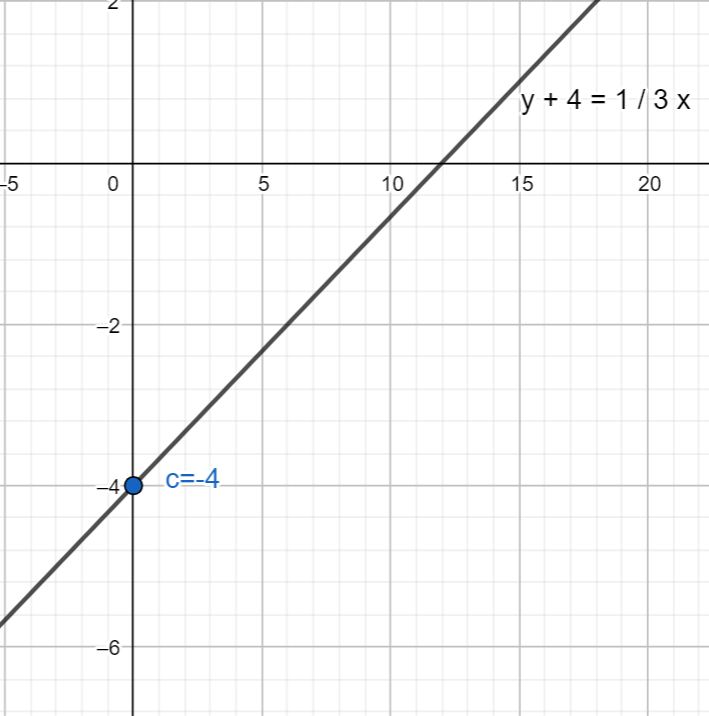
⇒(y+4)=31x
Therefore, the required equation is (y+4)=31x.
Note: We should know that the formula for the equation of slope point form is (y−y1)=m(x−x1), where we should have a slope and a point to find the required equation. We may not be given a direct value to be substituted instead we should find the data required for the equation from the given data.
