Question

How do you write an equation in point slope form parallel to$- 2x - 3y = - 2$ and passing through $\left( {2, - 2} \right)$?

Answer 1

In order to determine the slope and intercept to the above equation first rewrite the equation in such a way that the left side of the equation contain only variable $y$ ,$y = - \dfrac{3}{7}x + \dfrac{4}{7}$ and compare with the slope-intercept form $y = mx + c$, m is the slope and c is the y-intercept.

Complete step by step answer:
We are given an equation of line as $- 2x - 3y = - 2$ and a point $\left( {2, - 2} \right)$.
In this question we are supposed to find out the equation of line which is parallel to the equation of line $- 2x - 3y = - 2$ and passing through the point $\left( {2, - 2} \right)$.
For this we have to first determine the slope of the line $- 2x - 3y = - 2$.To do so , rewrite the equation of line into the general equation as $y = mx + c$where $m$is the slope of the line.
Rewriting the equation,
$\Rightarrow - 2x - 3y = - 2 \\\ \Rightarrow - 3y = 2x - 2 \\\ \Rightarrow y = - \dfrac{{2x}}{3} + \dfrac{2}{3} \\\$
Comparing the above result with the general equation $y = mx + c$,we have the slope of line $- 2x - 3y = - 2$equal to $m = - \dfrac{2}{3}$.
Thus, the slope of line parallel to line $- 2x - 3y = - 2$ will also have its slope as $m = - \dfrac{2}{3}$.
The Point-Slope Formula of straight line is
$\left( {y - {y_1}} \right) = m\left( {x - {x_1}} \right)$ where $\left( {{x_1},{y_1}} \right)$ is the point on the line.
So, we have the slope of the required line as $m = - \dfrac{2}{3}$ and also it is passing through the point$\left( {2, - 2} \right)$.We can write the equation of straight line using the point slope form as
$\Rightarrow \left( {y - \left( { - 2} \right)} \right) = - \dfrac{2}{3}\left( {x - 2} \right) \\\ \Rightarrow \left( {y + 2} \right) = - \dfrac{2}{3}\left( {x - 2} \right) \\\$
Multiplying both sides of the above equation with 3, we get
$\Rightarrow 3 \times \left( {y + 2} \right) = 3 \times \left( { - \dfrac{2}{3}\left( {x - 2} \right)} \right) \\\ \Rightarrow 3y + 6 = - 2\left( {x - 2} \right) \\\ \Rightarrow 3y + 6 = - 2x + 4 \\\$
combining all the like terms and rewrite the equation into the general equation form as $y = mx + c$, we can obtain the above equation as
$\Rightarrow 3y = - 2x + 4 - 6 \\\ \Rightarrow 3y = - 2x - 2 \\\ \Rightarrow y = \dfrac{{ - 2x}}{3} - \dfrac{2}{3} \\\$
Therefore, the equation of line parallel to $- 2x - 3y = - 2$ and passing through the point $\left( {2, - 2} \right)$ is equal to $y = \dfrac{{ - 2x}}{3} - \dfrac{2}{3}$.

Additional Information:
1.Cartesian Plane: A Cartesian Plane is given its name by the French mathematician Rene Descartes ,who first used this plane in the field of mathematics .It is defined as the two mutually perpendicular number line , the one which is horizontal is given name x-axis and the one which is vertical is known as y-axis. With the help of these axes we can plot any point on this cartesian plane with the help of an ordered pair of numbers.
2.Slope-Intercept Form = $y = mx + c$

Note: 1. The graph of both the lines is shown below.
The red line is the graph of equation $- 2x - 3y = - 2$and
The blue line is graph of equation $y = \dfrac{{ - 2x}}{3} - \dfrac{2}{3}$
.
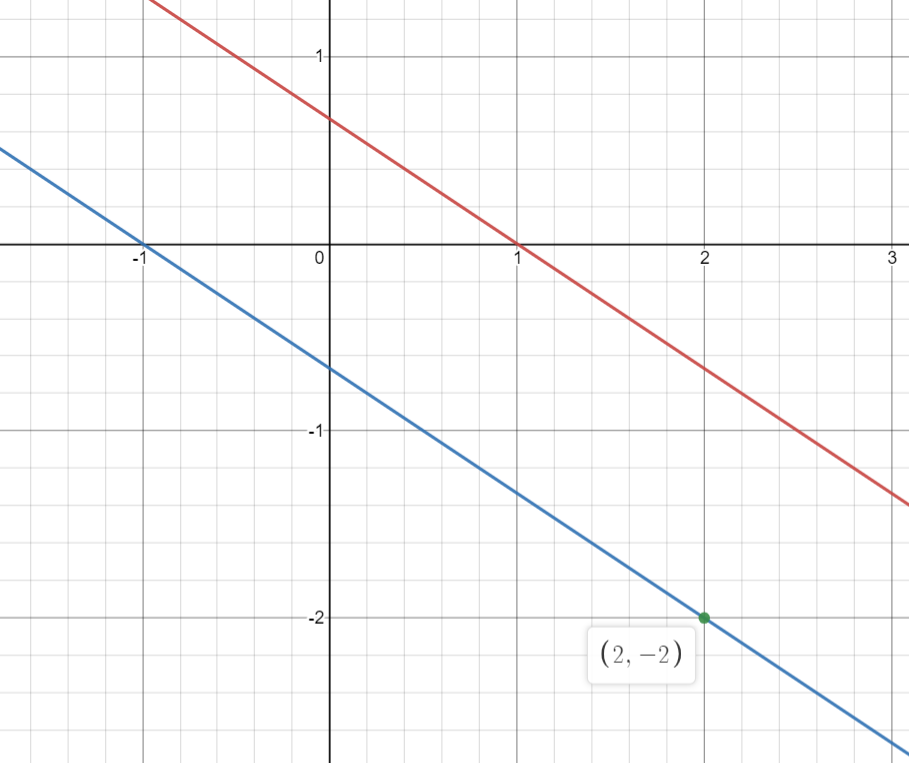
You can verify the result as the both the lines are parallel to each other.
2.Slope of line perpendicular to the line having slope $m$is equal to $- \dfrac{1}{m}$.
3.We should have a better knowledge in the topic of geometry to solve this type of question easily. We should know the Point-slope form $\left( {y - {y_1}} \right) = m\left( {x - {x_1}} \right)$ where $\left( {{x_1},{y_1}} \right)$ is the point on the line $m$as the form and also the Slope-intercept form of line as $y = mx + c$ where $m$ is the slope of the line