Question

: How do you write an equation for each line in point-slope form and slope-intercept form if slope =4, passing through $\left( 1,3 \right)$?

Answer 1

There are many forms to express the equation of a straight line, one of them is the slope-intercept form. The slope intercept form of a line is $y=mx+b$, here m is the slope of the line and b is the Y-intercept of the line. We can find the equation of the line by substituting values of the m, and b in the given equation.

Complete step by step answer:
We are asked to find the equation of the straight line with slope value as 4 and which passes through $\left( 1,3 \right)$. We will use the slope intercept form of the equation of a straight line for which the value of m is 4. The slope intercept form of the equation is $y=mx+b$ here m is the slope of the line and b is the Y-intercept of the line.
Substituting the values of the variables m in the slope intercept form of the equation, we get
$\Rightarrow y=4x+b$
This equation still has an unknown constant. To find the value of this constant, we will use the other information about the line. As the line passes through the point $\left( 1,3 \right)$, this point must satisfy the equation of the line. Substituting the point in the equation, we get
$\Rightarrow 3=4(1)+b$
Solving the above equation, we get
$\Rightarrow b=-1$
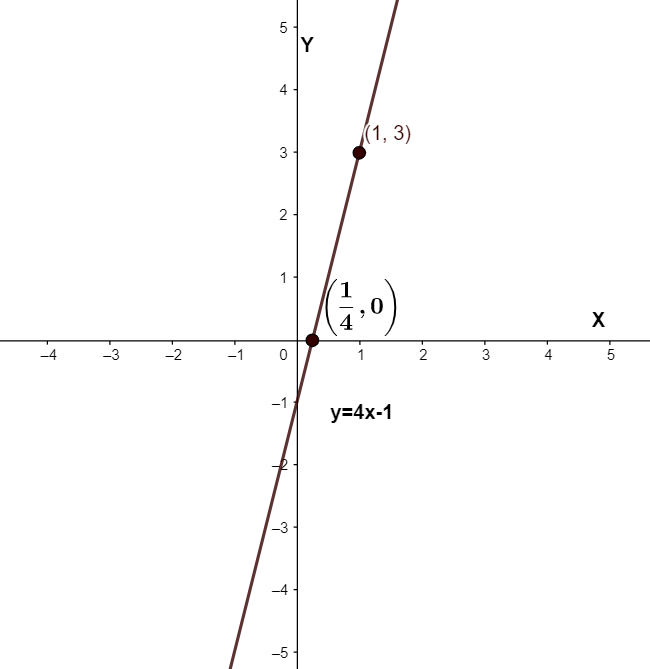
Now we have values of both m and b, hence, the slope intercept form of the equation is $y=4x-1$.
We can also graph the equation as follows:

Note: We can express the straight line in its different forms like standard form, intercept form etc. using the slope intercept form of the equation. The standard form of the equation of a straight line is $ax+by+c=0$. And the intercept form of the equation of straight line is $\dfrac{x}{a}+\dfrac{y}{b}=1$, for this form a, and b are X-intercept and Y-intercept respectively.