Question
Question: How do you write an equation for a hyperbola with vertices \[\left( 1,3 \right)\] and \[\left( -5,3 ...
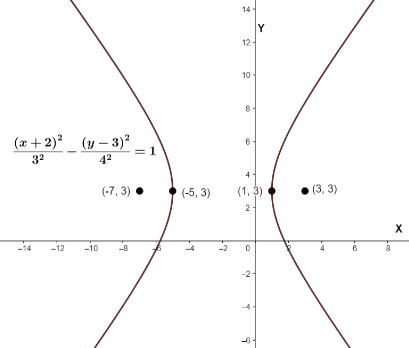
How do you write an equation for a hyperbola with vertices (1,3) and (−5,3), and foci (3,3) and (−7,3)?
Solution
To solve the given question, we should know the standard form of the hyperbola which is expressed as a2(x−h)2−b2(y−k)2=1. By substituting the values of all the variables, we can write the equation for a hyperbola. For the given standard hyperbola, the point of vertices can be expressed as (h−a,k)&(h+a,k). Similarly, we can find the coordinates of foci as (h−c,k)&(h+c,k). Here the relation between a,b&c can be expressed as a2+b2=c2. We will compare these coordinates with the given points to find the value of unknown variables.
Complete step by step answer:
The coordinates for the vertices are (1,3) and (−5,3) comparing these points with the coordinates of vertices of standard hyperbola (h−a,k)&(h+a,k). We get k=3, and other equations as −5=h−a and 1=h+a. Solving these two equations we get h=−2&a=3.
The coordinates for the foci are (3,3) and (−7,3), comparing these points with the coordinates of vertices of standard hyperbola (h−c,k)&(h+c,k). We already know the value of h and k from above equations, solving for c we get c=5.
Using the equation a2+b2=c2, we can find the value of b as 32+b2=52. On solving this we get b=4.
Using these values and substituting them in the standard form of general hyperbola, we can write the required equation as 32(x+2)2−42(y−3)2=1.
We can also plot the graph of the hyperbola as
Note: To solve these types of problems, we should know the equation as well as the properties of hyperbola. These properties include the coordinate of both vertices and both foci of the hyperbola. Calculation mistakes while solving these questions should be avoided.
