Solveeit Logo
Login

Question

Question: How do you write an equation (a) in slope-intercept form and (b) in standard form for the line passi...

How do you write an equation (a) in slope-intercept form and (b) in standard form for the line passing through (1,7)\left( 1,7 \right) and perpendicular to 3x+7y=13x+7y=1?

Explanation

Solution

The slope intercept form of a line is y=mx+by=mx+b, here m is the slope of the line and b is the Y-intercept of the line. We also have the standard form of the equation which is expressed as ax+by+c=0ax+by+c=0. To express an equation in this form, we have to take all terms to one side of the equation leaving zero to the other side. We should also know that the slope of a line perpendicular to a line with slope m equals −1m\dfrac{-1}{m}.

Complete step by step solution:
We are asked to find the equation of the straight and which is perpendicular to the line 3x+7y=13x+7y=1 and passes through (1,7)\left( 1,7 \right). We can easily find the slope of this given line as −37\dfrac{-3}{7}. The line we want to find is perpendicular to the given line, hence its slope value equals −1−37=73\dfrac{-1}{\dfrac{-3}{7}}=\dfrac{7}{3}.
We will use the slope intercept form of the equation of a straight line for which the value of m is 73\dfrac{7}{3}. The slope intercept form of the equation is y=mx+by=mx+b here m is the slope of the line and b is the Y-intercept of the line.
Substituting the values of the variable m in the slope intercept form of the equation, we get
⇒y=73x+b\Rightarrow y=\dfrac{7}{3}x+b
This equation has still an unknown constant. To find the value of this constant, we will use the other information about the line. As the line passes through the point (1,7)\left( 1,7 \right), this point must satisfy the equation of the line. Substituting the point in the equation, we get
⇒7=73(1)+b\Rightarrow 7=\dfrac{7}{3}(1)+b
Solving the above equation, we get
⇒b=143\Rightarrow b=\dfrac{14}{3}
(a) Now we have values of both m and b, hence, the slope intercept form of the equation isy=73x+143y=\dfrac{7}{3}x+\dfrac{14}{3}.
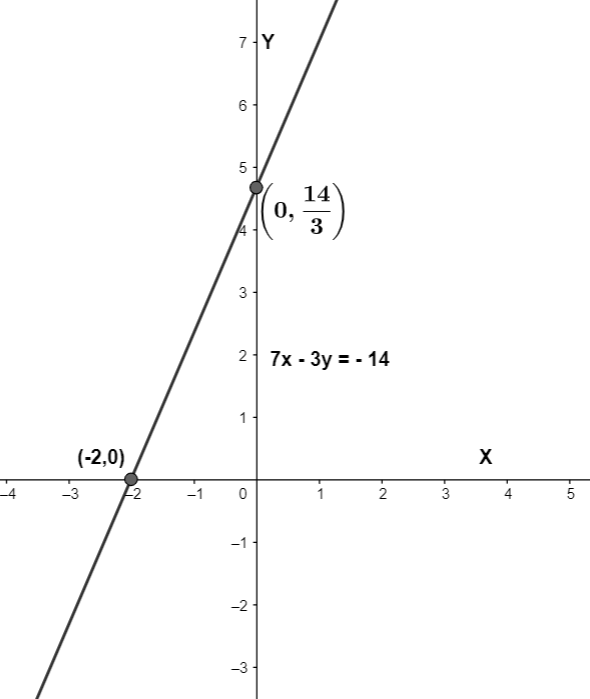
(b) To express this in standard form, we need to take all terms to one side and get rid of the fractions. The standard form of the equation is 7x−3y+14=07x-3y+14=0 or 7x−3y=−147x-3y=-14.
We can also graph the equation as follows:

Note: To solve these types of questions, we should know the properties of straight lines and its different forms of equation. The property of slopes should also be known, here we used the property of slopes of perpendicular lines which states that the slope of a line perpendicular to line with slope m equals −1m\dfrac{-1}{m}.