Solveeit Logo
Login

Question

Question: How do you write a vector CD as the sum of unit vectors for points \(C(7,4)\) and \(D(-8,-1)\) ?...

How do you write a vector CD as the sum of unit vectors for points C(7,4)C(7,4) and D(−8,−1)D(-8,-1) ?

Explanation

Solution

The difference in the positions between the two given points that are C(7,4)C(7,4) and D(−8,−1)D(-8,-1) with respect to the origin in the Cartesian coordinate plane will give us the vector CD as a sum of unit vectors. In the Cartesian plane, any point is described in the format P(x,y)P(x,y) where P is the point, xx is the horizontal distance of the point from the origin and yy is the vertical distance of the point from the origin.

Complete answer:
Let the origin be termed as O. Then, the coordinates of O are (0,0)(0,0).
Also, the coordinates of C and D are given to us as:
=C(7,4)=7i^+4j^ =D(−8,−1)=−8i^−j^ \begin{aligned} & =C(7,4)=7\widehat{i}+4\widehat{j} \\\ & =D(-8,-1)=-8\widehat{i}-\widehat{j} \\\ \end{aligned}
Therefore the vectors OC→\overrightarrow{OC} and OD→\overrightarrow{OD} can be given as:
⇒OC→=(7i^+4j^)−(0i^+0j^) ⇒OC→=7i^+4j^ \begin{aligned} & \Rightarrow \overrightarrow{OC}=(7\widehat{i}+4\widehat{j})-(0\widehat{i}+0\widehat{j}) \\\ & \Rightarrow \overrightarrow{OC}=7\widehat{i}+4\widehat{j} \\\ \end{aligned}
And,
⇒OD→=(−8i^−j^)−(0i^+0j^) ⇒OD→=−8i^−j^ \begin{aligned} & \Rightarrow \overrightarrow{OD}=(-8\widehat{i}-\widehat{j})-(0\widehat{i}+0\widehat{j}) \\\ & \Rightarrow \overrightarrow{OD}=-8\widehat{i}-\widehat{j} \\\ \end{aligned}
Now that we have obtained the values of OC→\overrightarrow{OC} and OD→\overrightarrow{OD} , we can easily calculate the value of CD→\overrightarrow{CD} using the Triangle Law of vector addition. The Triangle law of vector addition can be understood by the following diagram:

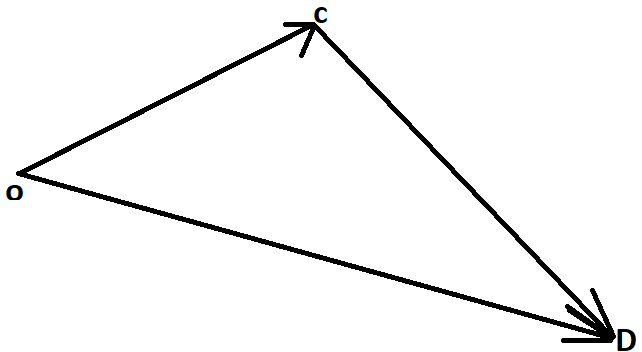
Here, the sum of vector OC and vector CD gives us the vector OD. Mathematically, it can be written as:
⇒OC→+CD→=OD→ ⇒CD→=OD→−OC→ \begin{aligned} & \Rightarrow \overrightarrow{OC}+\overrightarrow{CD}=\overrightarrow{OD} \\\ & \Rightarrow \overrightarrow{CD}=\overrightarrow{OD}-\overrightarrow{OC} \\\ \end{aligned}
Putting the values of vector OD and vector OC, we get Vector CD as:
⇒CD→=(−8i^−j^)−(7i^+4j^) ⇒CD→=−15i^−5j^ \begin{aligned} & \Rightarrow \overrightarrow{CD}=(-8\widehat{i}-\widehat{j})-(7\widehat{i}+4\widehat{j}) \\\ & \Rightarrow \overrightarrow{CD}=-15\widehat{i}-5\widehat{j} \\\ \end{aligned}
Hence, the vector CD as a sum of unit vectors is −15i^−5j^-15\widehat{i}-5\widehat{j} .

Note:
We saw the definition of a point in a cartesian system co-ordinate and then the application of triangle rule of vector addition. These are some key theorems and concepts in basic physics. Here, we could have performed the vector addition using the parallelogram method for vector addition too as both the theorems work on the same basic principle.