Question

How do you write a quadratic function in vertex form from whose graph has the vertex $\left( 1,8 \right)$ and passes through the point $\left( 3,12 \right)$?

Answer 1

In this question we have been given a vertex on a graph as $\left( 1,8 \right)$ and it passes through the point $\left( 3,12 \right)$. We will use the general format of the equation of a quadratic function in vertex form which is given by $y=a{{\left( x-h \right)}^{2}}+k$, where $\left( h,k \right)$ are the coordinates of the vertex and $a$ is a coefficient which is also called as the multiplier. We will substitute the coordinates of the vertex to get the equation and then substitute the coordinate of the point to find the value of $a$ and substitute it to get the required solution.

Complete step by step answer:
We know that the equation of a quadratic function in vertex form is given as $y=a{{\left( x-h \right)}^{2}}+k$, where $\left( h,k \right)$ are the coordinates of the vertex and $a$ is a coefficient.
On substituting the coordinate $\left( 1,8 \right)$ in the equation, we get:
$\Rightarrow y=a{{\left( x-1 \right)}^{2}}+8$
Now we know that this vertex passes through the point $\left( 3,12 \right)$ therefore, to get the value of $a$, we will substitute $\left( x,y \right)$ as $\left( 3,12 \right)$.
On substituting, we get:
$\Rightarrow 12=a{{\left( 3-1 \right)}^{2}}+8$
On simplifying the right-hand side, we get:
$\Rightarrow 12=a{{\left( 2 \right)}^{2}}+8$
On substituting ${{2}^{2}}=4$, we get:
$\Rightarrow 12=4a+8$
On transferring the term $8$ from the right-hand side to the left-hand side, we get:
$\Rightarrow 12-8=4a$
On simplifying, we get:
$\Rightarrow 4=4a$
On rearranging the equation, we get:
$\Rightarrow a=\dfrac{4}{4}$
On simplifying, we get:
$\Rightarrow a=1$
On substituting $a=1$ in the equation of vertex, we get:
$\Rightarrow y=1{{\left( x-1 \right)}^{2}}+8$
On simplifying, we get:
$\Rightarrow y={{\left( x-1 \right)}^{2}}+8$
On drawing it on the graph, we get:

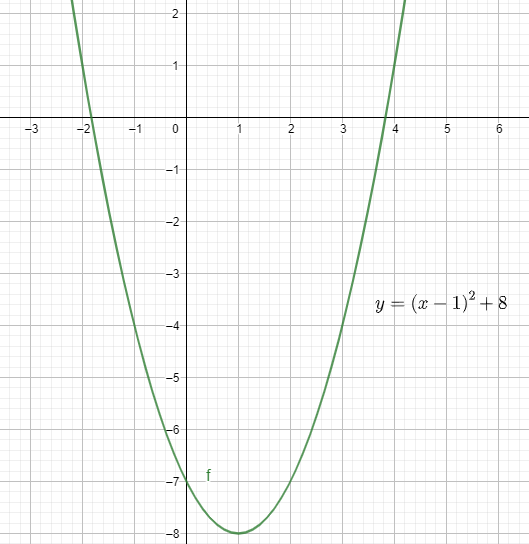
Which is the required solution.

Note: It is to be remembered that the vertex form is an alternate way of writing the equation of a parabola. We know that a quadratic equation is in the form $a{{x}^{2}}+bx+c$, which when graphed gives us a parabola. The value of the constant $a$ in the vertex form tells whether the parabola is going upwards or downwards. If $a$ is positive then parabola is going upwards else parabola is going downwards.