Question
Question: How do you write a quadratic equation with vertex \(\left( 2,1 \right)\) and y intercept \(\left( 0,...
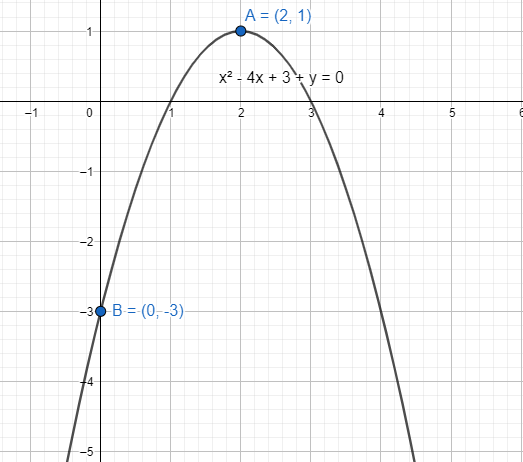
How do you write a quadratic equation with vertex (2,1) and y intercept (0,−3)?
Solution
We have to find the quadratic equation with vertex (2,1) and y intercept (0,−3). The equation will be a general equation of parabola. We equate the required equation of parabolic curve with the general equation of (x−α)2=4a(y−β). We put the values of y intercepts and the vertex coordinate.
Complete step by step answer:
The general equation (x−α)2=4a(y−β) is a parabolic curve.
For the general equation (α,β) is the vertex. 4a is the length of the latus rectum. The coordinate of the focus is (α,β+a).
This gives the vertex as (2,1). Putting the value in (x−α)2=4a(y−β), we get
(x−α)2=4a(y−β)⇒(x−2)2=4a(y−1)
We need to find the value of a.
We now find the Y-axis intercepts. In that case for the Y-axis, we have to take the coordinate values of x as 0. Putting the value of (0,−3) in the equation (x−2)2=4a(y−1), we get
(0−2)2=4a(−3−1)⇒−16a=4⇒4a=−44=−1
Putting value of 4a in the equation (x−2)2=4a(y−1), we get
(x−2)2=4a(y−1)⇒(x−2)2=−(y−1)=1−y
Now simplifying we get
(x−2)2=1−y⇒x2−4x+3+y=0
The quadratic equation is x2−4x+3+y=0.
Note:
The maximum point of the function (x−2)2+(y−1)=0 is (2,1). The graph is bounded at that point. But on the other side the curve is open and not bounded. The general case of parabolic curve is to be bounded at one side to mark the vertex.
