Question

How do you write a quadratic equation with Vertex $(5,5)$ and Point $(6,6)$ ?

Answer 1

Hint : Just as a quadratic equation can map a parabola, the parabola's points can help write a corresponding quadratic equation. Parabolas have two equation forms – standard and vertex. The vertex of a parabola is the point at the top or bottom of the parabola. Vertex form is useful, because it lets us pick out the vertex of a parabola really quickly just by looking at the equation.

Complete step by step solution:
In this given problem,
We have a quadratic equation with Vertex- $(5,5)$ and Point- $(6,6)$
For this question the two forms of a parabola's equation should be followed:
Standard form: $y = a{x^2} + bx + c$
Vertex form: $y = a{(x - h)^2} + k$ (with vertex at $(h,k)$ )
First, we use the values given in question to form vertex equation
$\Rightarrow y = a{(x - 5)^2} + 5$ Taking $h$ =5 and $k$ =5 since Vertex is $(5,5)$ …………..(1)
Now in order to find out $a$ we use the information given about Point- $(6,6)$ in above equation
$\Rightarrow 6 = a{(6 - 5)^2} + 5$
$\Rightarrow 6 = a + 5$
$\therefore a = 1$
Since we have all the information, we can use the standard form of to form a quadratic equation as follows from the vertex form in (1):
$\Rightarrow y = a{(x - 5)^2} + 5$
Substituting $a = 1$ ,
$\Rightarrow y = {(x - 5)^2} + 5$
Factoring ${(x - 5)^2}$ with the help of formula:
${(a - b)^2} = {a^2} - 2ab + {b^2}$
Substituting $a = x$ and $b = 5$ we get,
$\Rightarrow y = ({x^2} - 10x + 25) + 5$
Opening the brackets,
$\Rightarrow y = {x^2} - 10x + 25 + 5$
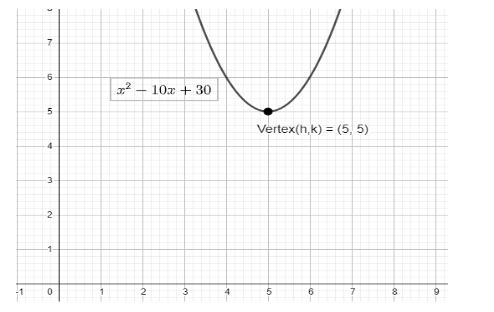
$\therefore y = {x^2} - 10x + 30$
Hence, we get the final quadratic equation as: $y = {x^2} - 10x + 30$.

Note : A parabolic equation resembles a quadratic equation in appearance. You can find the vertex and standard forms of a parabolic equation and write the parabola algebraically with only two of the parabola's points, the vertex and one other.
The vertex $(5,5)$ of given equation is shown graphically for better understanding:

Remember to use the vertex form of equation first and find out the missing data to arrive at the standard equation form.