Solveeit Logo
Login

Question

Question: How do you write a quadratic equation in intercept form whose graph has x intercepts \(-3,-2\) and p...

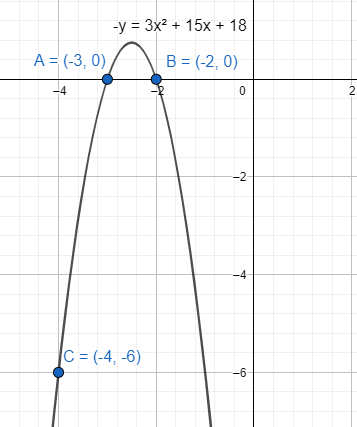
How do you write a quadratic equation in intercept form whose graph has x intercepts −3,−2-3,-2 and passes through (−4,−6)\left( -4,-6 \right)?

Explanation

Solution

We equate the given equation of parabolic curve with the general equation of y=ax2+bx+cy=a{{x}^{2}}+bx+c. We put the values of x intercepts and also the value of the point (−4,−6)\left( -4,-6 \right) through which the curve is passing. We find the value of the variables and get the equation.

Complete step by step answer:
The general equation of a quadratic is y=ax2+bx+cy=a{{x}^{2}}+bx+c. We have three variables of a,b,ca,b,c.
We have been given three conditions to solve the variables.
The graph has x intercepts −3,−2-3,-2 and passes through (−4,−6)\left( -4,-6 \right).
The x intercept points will be (−3,0),(−2,0)\left( -3,0 \right),\left( -2,0 \right).
So, first we put the values for (−3,0),(−2,0)\left( -3,0 \right),\left( -2,0 \right) in the equation y=ax2+bx+cy=a{{x}^{2}}+bx+c.
For (−3,0)\left( -3,0 \right) we get
0=a(−3)2+b×(−3)+c ⇒0=9a−3b+c ⇒c=3b−9a \begin{aligned} & 0=a{{\left( -3 \right)}^{2}}+b\times \left( -3 \right)+c \\\ & \Rightarrow 0=9a-3b+c \\\ & \Rightarrow c=3b-9a \\\ \end{aligned}
For (−2,0)\left( -2,0 \right) we get
0=a(−2)2+b×(−2)+c ⇒0=4a−2b+c ⇒c=2b−4a \begin{aligned} & 0=a{{\left( -2 \right)}^{2}}+b\times \left( -2 \right)+c \\\ & \Rightarrow 0=4a-2b+c \\\ & \Rightarrow c=2b-4a \\\ \end{aligned}
We get two values for cc and equating them we get
3b−9a=2b−4a ⇒b=5a \begin{aligned} & 3b-9a=2b-4a \\\ & \Rightarrow b=5a \\\ \end{aligned}
So, c=3×5a−9a=6ac=3\times 5a-9a=6a
Now we put the value (−4,−6)\left( -4,-6 \right) in the equation y=ax2+bx+cy=a{{x}^{2}}+bx+c.
−6=a(−4)2+b×(−4)+c ⇒−6=16a−4b+c ⇒c=4b−16a−6 \begin{aligned} & -6=a{{\left( -4 \right)}^{2}}+b\times \left( -4 \right)+c \\\ & \Rightarrow -6=16a-4b+c \\\ & \Rightarrow c=4b-16a-6 \\\ \end{aligned}
Putting all the values we get
c=4b−16a−6 ⇒6a=20a−16a−6 ⇒−2a=6 ⇒a=−3 \begin{aligned} & c=4b-16a-6 \\\ & \Rightarrow 6a=20a-16a-6 \\\ & \Rightarrow -2a=6 \\\ & \Rightarrow a=-3 \\\ \end{aligned}
The values for bb and cc is 5×(−3)=−155\times \left( -3 \right)=-15 and 6×(−3)=−186\times \left( -3 \right)=-18 respectively.
The equation becomes y=−3x2−15x−18y=-3{{x}^{2}}-15x-18. This is a parabola.
The simplified form is (x+52)2=−13(y−34){{\left( x+\dfrac{5}{2} \right)}^{2}}=-\dfrac{1}{3}\left( y-\dfrac{3}{4} \right).

Note:
The minimum point of the function y=−3x2−15x−18y=-3{{x}^{2}}-15x-18 is (−52,34)\left( -\dfrac{5}{2},\dfrac{3}{4} \right). The graph is bounded at that point. But on the other side the curve is open and not bounded. The general case of parabolic curve is to be bounded at one side to mark the vertex.