Question

How do you write $5x-3y=24$ in slope-intercept form?

Answer 1

The general form of a straight line is given as $ax+by+c=0$ where slope is given as $\dfrac{-a}{b}$ , $x$ intercept is given as $\dfrac{-c}{b}$ and $y$ intercept is given as $\dfrac{-c}{a}$ . The slope intercept form of a straight line is given as $y=mx+c$ where $m$ is the slope and $c$ is the $y$ intercept.

Complete step by step solution:
Now considering from the question we have been asked to write the given straight line expression $5x-3y=24$ in the slope intercept form
From the basics of concept we know that the general form of a straight line is given as $ax+by+c=0$ where slope is given as $\dfrac{-a}{b}$ , $x$ intercept is given as $\dfrac{-c}{b}$ and $y$ intercept is given as $\dfrac{-c}{a}$ .
The slope intercept form of a straight line is given as $y=mx+c$ where $m$ is the slope and $c$ is the $y$ intercept.
Hence this expression has slope is $\dfrac{5}{3}$ and $y$ intercept is $-8$ .
Therefore the slope-intercept form of the given expression $5x-3y=24$ is given as $y=\dfrac{5}{3}x-8$ .
The graph of this expression will be as shown below:

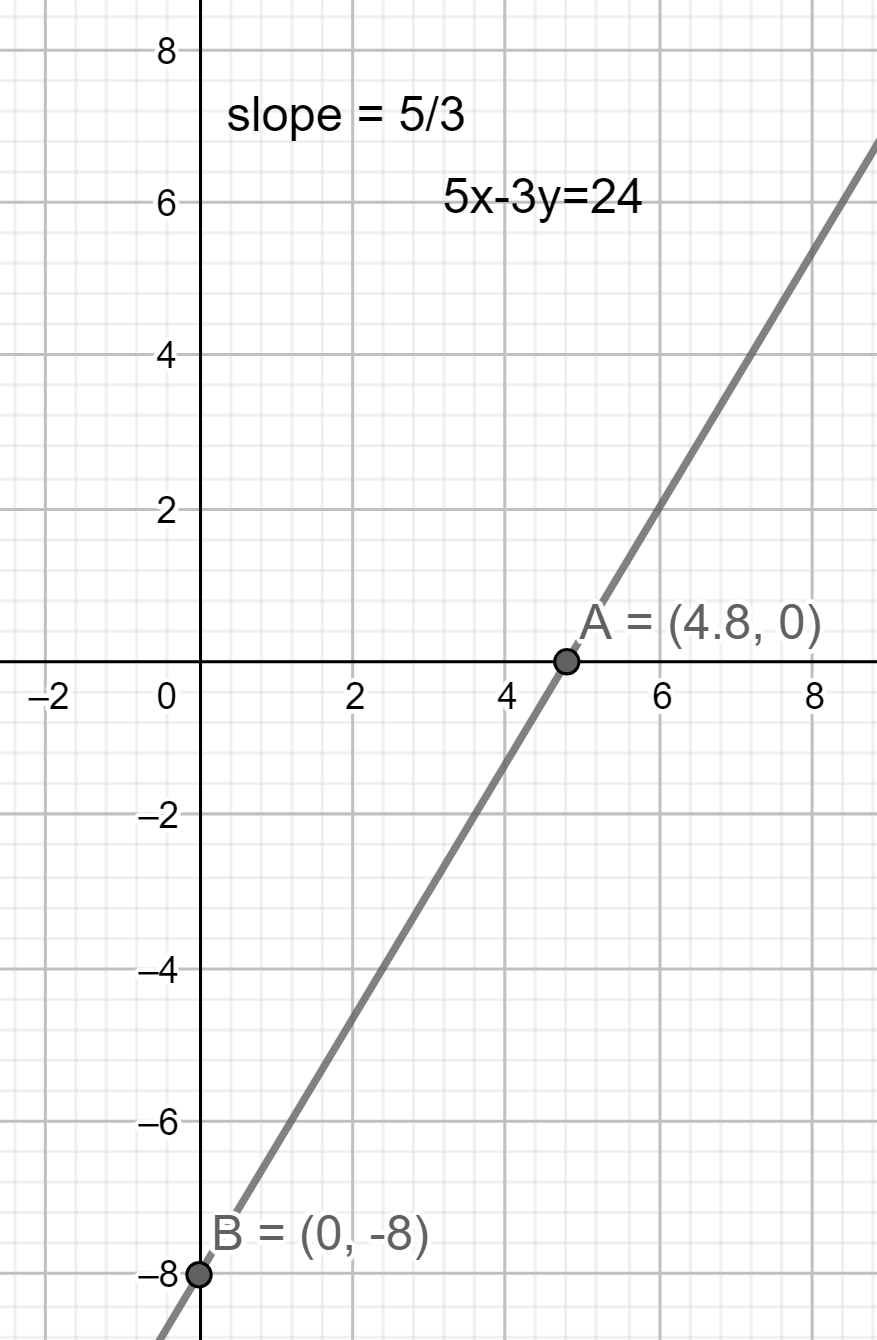
Note: While drawing the graph of the given expression we should mark the points accurately and join them exactly in order to obtain an appropriate graph. We can also answer this question simply by not finding any intercepts or slopes. That is as the given expression is $5x-3y=24$ we need to simplify it. After simplifying we will have
$\begin{aligned} & \Rightarrow 5x-24=3y \\\ & \Rightarrow y=\dfrac{5x-24}{3} \\\ & \Rightarrow y=\dfrac{5}{3}x-8 \\\ \end{aligned}$
We can observe that we have got the same answer in both the cases.