Question

How do you verify the identity $\cot \left( {\dfrac{\pi }{2} - x} \right) = \tan x$?

Answer 1

Use the angle sum property of a triangle and definitions of trigonometric ratios with respect to an acute angle in a right angled triangle to deduce the given identity.

Complete step-by-step solution:
Consider a right angled triangle with right angle at $\angle B$ and $\angle C = x$.

It is known that the sum of all interior angles of a triangle is $\pi$ radian.
$\angle A + \angle B + \angle C = \pi$

Substitute $\angle B$ as $\dfrac{\pi }{2}$ radian and $\angle C$ as $x$ radian to obtain the expression for $\angle A$ as shown below.
$\Rightarrow \angle A + \dfrac{\pi }{2} + x = \pi$
$\Rightarrow \angle A = \dfrac{\pi }{2} - x$

Therefore, the $\angle A$ can be expressed as $\left( {\dfrac{\pi }{2} - x} \right)$ radian.
The right triangle with right angle at $\angle B$, $\angle C = x$ and so $\angle A = \dfrac{\pi }{2} - x$ is shown in the figure below.

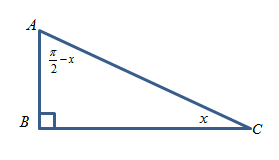
Now, use the definition of trigonometric ratio for $\tan x$ and $\cot \left( {\dfrac{\pi }{2} - x} \right)$ to solve further.
For an angle $x$ as argument, side $AB$ act as perpendicular (side in front of the argument angle), side $BC$ act as base and side $AC$ always be hypotenuse for this triangle.

Therefore, the trigonometry ratio $\tan x$ defined as the ratio of perpendicular to the base is written as,
$\tan x = \dfrac{P}{B}$
$\Rightarrow \tan x = \dfrac{{AB}}{{BC}}$ …… (1)

For angle $\left( {\dfrac{\pi }{2} - x} \right)$ as argument, side $BC$ act as perpendicular (side in front of the argument angle), side $AB$ act as base and side $AC$ always be hypotenuse for this triangle.

Therefore, the trigonometry ratio $\cot \left( {\dfrac{\pi }{2} - x} \right)$ defined as the ratio of base to the perpendicular is written as,

$\cot \left( {\dfrac{\pi }{2} - x} \right) = \dfrac{B}{P}$
$\Rightarrow \cot \left( {\dfrac{\pi }{2} - x} \right) = \dfrac{{AB}}{{BC}}$ …… (2)

From the equation (1) and (2), it is verified that $\cot \left( {\dfrac{\pi }{2} - x} \right) = \tan x$.

Note: Angle $\dfrac{\pi }{2}$ radian is equivalent to $90^\circ$ degree. The transformation of angle in degree to angle in radian can be done by the use of relation $\pi \,rad = 180^\circ$.
There are few other trigonometric identities similar to the given identity.
The relation between sine and cosine ratio in terms of conjugate angles is shown below.
$\Rightarrow \sin \left( {\dfrac{\pi }{2} - x} \right) = \cos x$
$\Rightarrow \cos \left( {\dfrac{\pi }{2} - x} \right) = \sin x$
The relation between cosecant and secant ratio in terms of conjugate angles is shown below.
$\Rightarrow \cos ec\left( {\dfrac{\pi }{2} - x} \right) = \sec x$
$\Rightarrow \sec \left( {\dfrac{\pi }{2} - x} \right) = \cos ecx$