Solveeit Logo
Login

Question

Question: How do you verify \( {\sec ^2}\left( {\dfrac{\pi }{2} - x} \right) - 1 = {\cot ^2}x? \)...

How do you verify sec⁡2(π2−x)−1=cot⁡2x?{\sec ^2}\left( {\dfrac{\pi }{2} - x} \right) - 1 = {\cot ^2}x?

Explanation

Solution

Hint : We shall solve the above question with the help of one of the three Pythagorean trigonometric identities: tan⁡2θ+1=sec⁡2θ{\tan ^2}\theta + 1 = {\sec ^2}\theta .
Pythagorean identities:

sin⁡2θ+cos⁡2θ=1 1+tan⁡2θ=sec⁡2θ 1+cot⁡2θ=csc⁡2θ   {\sin ^2}\theta + {\cos ^2}\theta = 1 \\\ 1 + {\tan ^2}\theta = {\sec ^2}\theta \\\ 1 + {\cot ^2}\theta = {\csc ^2}\theta \;

Complete step by step solution:
The given question is to verify sec⁡2(π2−x)−1=cot⁡2x{\sec ^2}\left( {\dfrac{\pi }{2} - x} \right) - 1 = {\cot ^2}x .
To prove this, let us first prove the Pythagorean trigonometric identity tan⁡2θ+1=sec⁡2θ{\tan ^2}\theta + 1 = {\sec ^2}\theta .
Consider the below diagram where the point (x,y)(x,y) defines an angle θ\theta at the origin and rr is the distance from the origin to the point (x,y)(x,y) .

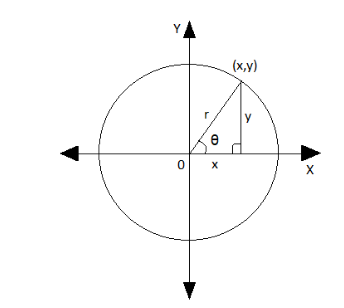
From the above diagram, we can make use of Pythagoras’ theorem to obtain
y2+x2=r2{y^2} + {x^2} = {r^2}
Divide throughout by r2{r^2} ,
⇒y2r2+x2r2=1\Rightarrow \dfrac{{{y^2}}}{{{r^2}}} + \dfrac{{{x^2}}}{{{r^2}}} = 1
We know that from the diagram,
y2r2=sin⁡2θ\dfrac{{{y^2}}}{{{r^2}}} = {\sin ^2}\theta and x2r2=cos⁡2θ\dfrac{{{x^2}}}{{{r^2}}} = {\cos ^2}\theta
Hence, the expression becomes,
sin⁡2θ+cos⁡2θ=1{\sin ^2}\theta + {\cos ^2}\theta = 1 , this is an important identity.
Now, let us divide throughout by cos⁡2θ{\cos ^2}\theta
⇒sin⁡2θcos⁡2θ+cos⁡2θcos⁡2θ=1cos⁡2θ\Rightarrow \dfrac{{{{\sin }^2}\theta }}{{{{\cos }^2}\theta }} + \dfrac{{{{\cos }^2}\theta }}{{{{\cos }^2}\theta }} = \dfrac{1}{{{{\cos }^2}\theta }}
On further simplification we get,
tan⁡2θ+1=sec⁡2θ{\tan ^2}\theta + 1 = {\sec ^2}\theta
Let us replace θ\theta by π2−x\dfrac{\pi }{2} - x
⇒tan⁡2(π2−x)+1=sec⁡2(π2−x)\Rightarrow {\tan ^2}\left( {\dfrac{\pi }{2} - x} \right) + 1 = {\sec ^2}\left( {\dfrac{\pi }{2} - x} \right)
Subtracting 11 from both the sides
⇒tan⁡2(π2−x)=sec⁡2(π2−x)−1\Rightarrow {\tan ^2}\left( {\dfrac{\pi }{2} - x} \right) = {\sec ^2}\left( {\dfrac{\pi }{2} - x} \right) - 1
We know that tan⁡(π2−θ)=cot⁡θ\tan \left( {\dfrac{\pi }{2} - \theta } \right) = \cot \theta
Hence, sec⁡2(π2−x)−1=cot⁡2x{\sec ^2}\left( {\dfrac{\pi }{2} - x} \right) - 1 = {\cot ^2}x

Note : Trigonometric identities used in the above solutions are Reciprocal identities, Pythagorean identities and Quotient identities. These identities are given below:
Reciprocal identities:
sin⁡θ=1csc⁡θ cos⁡θ=1sec⁡θ tan⁡θ=1cot⁡θ   \sin \theta = \dfrac{1}{{\csc \theta }} \\\ \cos \theta = \dfrac{1}{{\sec \theta }} \\\ \tan \theta = \dfrac{1}{{\cot \theta }} \;
Pythagorean identities:

sin⁡2θ+cos⁡2θ=1 1+tan⁡2θ=sec⁡2θ 1+cot⁡2θ=csc⁡2θ   {\sin ^2}\theta + {\cos ^2}\theta = 1 \\\ 1 + {\tan ^2}\theta = {\sec ^2}\theta \\\ 1 + {\cot ^2}\theta = {\csc ^2}\theta \;

Quotient identities:
sin⁡θcos⁡θ=tan⁡θ cos⁡θsin⁡θ=cot⁡θ   \dfrac{{\sin \theta }}{{\cos \theta }} = \tan \theta \\\ \dfrac{{\cos \theta }}{{\sin \theta }} = \cot \theta \;
There are two more identities other than these. They are Cofunction identities and Even Odd identities.
∙\bullet Learn these formulas that are given above well, so that it will be easier to recognize what procedure and steps are followed in solving such questions.
∙\bullet First, simplify the most complex side so that it has the same form as the simplest side.
That is, first start simplifying on one side and make it look like the other side.
∙\bullet If the given question contains a squared term, then we make use of one of the Pythagorean identities which was mentioned earlier.