Question

How do you use transformation to graph the sine function and determine the amplitude and period of $y=\sin \left( 3x \right)$?

Answer 1

This question is from the topic of trigonometry. In this question, we will draw the function of sin(3x) and then, find the amplitude and period of $y=\sin \left( 3x \right)$. In solving this question, we will first know the general form of sin function. From, we will understand the amplitude, phase shift, vertical shift and then period. After that, we will find the value amplitude and period. After that, we will draw the graph.

Complete step by step solution:
Let us solve this question.
In this question, we have asked to find the amplitude and period of $y=\sin \left( 3x \right)$. And, also we have to draw the graph for the same.
So, let us first know about the general form of sin function for finding the amplitude and period.
The general form is:
$y=a\sin \left( bx+c \right)+d$
Here, ‘a’ is amplitude, $\dfrac{2\pi }{b}$ is period, $\left( -\dfrac{c}{b} \right)$ is phase shift or we can say that the graph is being shifted by $\left( -\dfrac{c}{b} \right)$ units towards x-axis, and ‘d’ is the vertical shift or we can say that the graph is shifted by ‘d’ units towards y-axis.
So, from the equation $y=\sin x$, we can say that the amplitude is 1 and period is $2\pi$.
Similarly, in the equation, we can say in the equation $y=\sin \left( 3x \right)$ that the amplitude is 1 as same as in $y=\sin x$ and period is $\dfrac{2\pi }{b}=\dfrac{2\pi }{3}$. And, phase and vertical shift will be zero as the value of c and d are zero.
Now, we will see the graph for the equation $y=\sin x$ and $y=\sin \left( 3x \right)$ in the following:

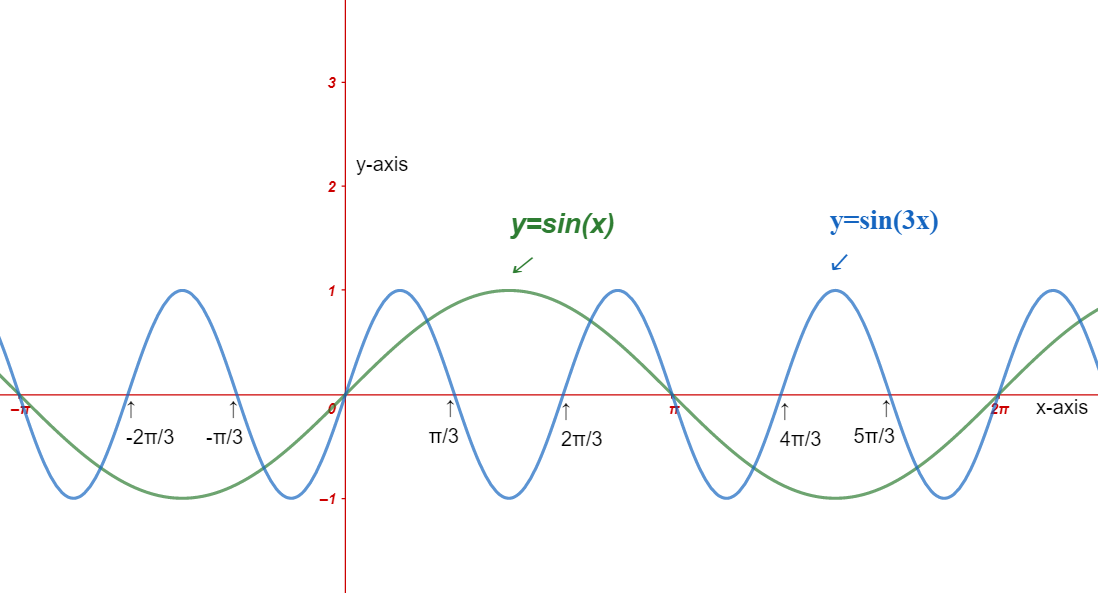
Here, we can see that in the function $y=\sin \left( 3x \right)$, the amplitude is 1 that is same as $y=\sin x$ but the $y=\sin x$ function has period of $2\pi$ and the function $y=\sin \left( 3x \right)$ is having a period of $\dfrac{2\pi }{3}$.

Note: We should have a better knowledge in the topic of trigonometry to solve this type of question easily. We should know the general form of sin function. The general form is:
$y=a\sin \left( bx+c \right)+d$
Where, ‘a’ is amplitude, ‘d’ is the vertical shift, $\left( -\dfrac{c}{b} \right)$ is the phase shift, and $\dfrac{2\pi }{b}$ is period.