Question

How do you use the unit circle to find the exact value of $\cos \left( \dfrac{7\pi }{3} \right)$?

Answer 1

To solve these types of problems, we should know some of the trigonometric properties. The first one is, $\cos (2\pi +x)=\cos x$. This is true because when a point completes one rotation and comes back in the first quadrant its reference angle equals $\theta -2\pi$, where $\theta$ is the total angle rotated by the point.

Complete answer:

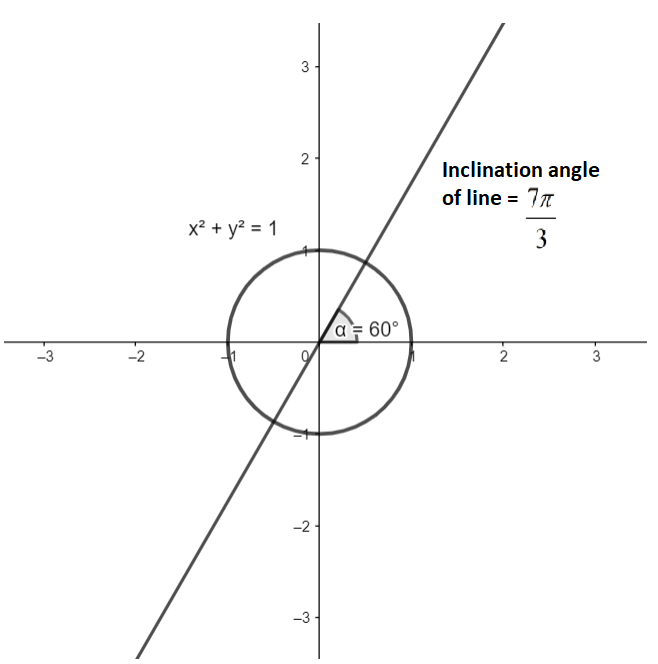
We are asked to find the value of the $\cos \left( \dfrac{7\pi }{3} \right)$. From the given figure we can see that the unit circle and the coordinate axes have divided the coordinate plane into 4 sectors. Each of those sectors is the quadrant of the coordinate axes.
As we can see that the line with the inclination $\dfrac{7\pi }{3}$, lies in the first quadrant. As it has completed a full rotation before coming back in the first sector. The angle can be written in the form of $2\pi +x$. Comparing this with the inclination of the line, we get
$\Rightarrow 2\pi +x=\dfrac{7\pi }{3}$
Subtracting $2\pi$ from both sides of the above equation, we get

& \Rightarrow 2\pi +x-2\pi =\dfrac{7\pi }{3}-2\pi \\\ & \Rightarrow x=\dfrac{\pi }{3} \\\ \end{aligned}$$ we want to find the value of $$\cos \left( \dfrac{7\pi }{3} \right)$$. As we have seen the angle $$\dfrac{7\pi }{3}$$ can also be written as $$2\pi +\dfrac{\pi }{3}$$. Using this in the evaluation of the value of the $$\cos \left( \dfrac{7\pi }{3} \right)$$, we get $$\Rightarrow \cos \left( \dfrac{7\pi }{3} \right)=\cos \left( 2\pi +\dfrac{\pi }{3} \right)$$ We know the property $$\cos (2\pi +x)=\cos x$$, using this in the for the above expression we get $$\Rightarrow \cos \left( 2\pi +\dfrac{\pi }{3} \right)=\cos \left( \dfrac{\pi }{3} \right)$$ As we know that the value of $$\cos \left( \dfrac{\pi }{3} \right)$$ is $$\dfrac{1}{2}$$. Hence, the value of $$\cos \left( \dfrac{7\pi }{3} \right)$$ equals $$\dfrac{1}{2}$$. **Note:** The line drawn in the figure is just for reference, it is to show the angle of inclination $$\dfrac{7\pi }{3}$$. The question can be solved without it. Also, to solve these types of problems, one should know the trigonometric properties of the ratios.