Question

How do you use the shell method to set up and evaluate the integral that gives the volume of the solid generated by revolving the plane region $y = 6x + 7$ and $y = {x^2}$ rotated about the line $y = 49$ ?

Answer 1

Hint : We have to find the volume of the solid generated by revolving the plane region $y = 6x + 7$ and $y = {x^2}$ rotated about the line $y = 49$ using the shell method. Shell method is based on the assumption that a solid can be divided into many cylinders with infinitesimal heights and the volume of a solid can be written as the sum of the volumes of these small cylinders. To find the required volume we have to find the volume of a general small cylinder or shell in the solid and then integrate over the required range.

Complete step by step solution:
We have to find the volume of the solid generated by revolving the region $y = 6x + 7$ and $y = {x^2}$ rotated about the line $y = 49$ . We have to use the shell method for this. The graph of the given functions is as follows,

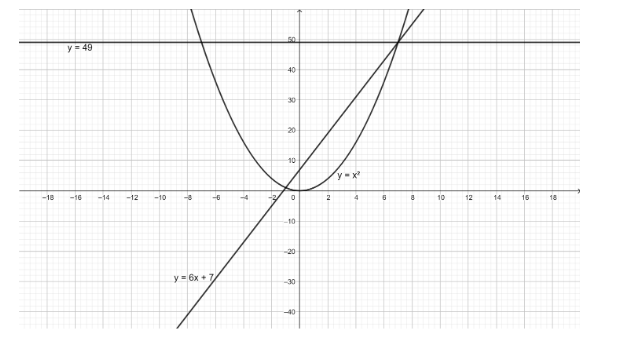
We have to assume cylindrical shells for the solid figure and then integrate over the range to get the final volume. For vertical cylindrical shells this is given as,
$V = \int\limits_a^b {2\pi rf\left( y \right)dy}$
Since the cylinder revolves around $y = 49$ , the radius of the cylindrical shell will be $r = \left( {49 - y} \right)$ .
The given two curves $y = 6x + 7$ and $y = {x^2}$ meet at $\left( { - 1,1} \right)$ and $\left( {7,49} \right)$ .
Now, for $y = 0$ to $1$ , $x$ varies from $- \sqrt y$ to $\sqrt y$ .
And for $y = 1$ to $49$ , $x$ varies from $\dfrac{{y - 7}}{6}$ to $\sqrt y$ .
Thus, the required volume can be written as,
$V = \int\limits_0^1 {2\pi \left( {49 - y} \right)\left( {\sqrt y - \left( { - \sqrt y } \right)} \right)dy + } \int\limits_1^{49} {2\pi \left( {49 - y} \right)\left( {\sqrt y - \left( {\dfrac{{y - 7}}{6}} \right)} \right)dy}$
We can solve the integral to find the volume.

$$\Rightarrow V = \int\limits_0^1 {2\pi \left( {49 - y} \right)\left( {2\sqrt y } \right)dy + } \int\limits_1^{49} {2\pi \left( {49 - y} \right)\left( {\sqrt y - \left( {\dfrac{y}{6} - \dfrac{7}{6}} \right)} \right)dy} \\\ \Rightarrow V = \int\limits_0^1 {4\pi \left( {49{y^{\dfrac{1}{2}}} - {y^{\dfrac{3}{2}}}} \right)dy + } \int\limits_1^{49} {2\pi \left( {49{y^{\dfrac{1}{2}}} - \dfrac{{49y}}{6} + \dfrac{{343}}{6} - {y^{\dfrac{3}{2}}} + \dfrac{{{y^2}}}{6} - \dfrac{{7y}}{6}} \right)dy} \\\ \Rightarrow V = 4\pi \left[ {49.\dfrac{2}{3}{y^{\dfrac{3}{2}}} - \dfrac{2}{5}{y^{\dfrac{5}{2}}}} \right]_0^1 + 2\pi \left[ {49.\dfrac{2}{3}{y^{\dfrac{3}{2}}} - \dfrac{{49}}{6}\dfrac{{{y^2}}}{2} + \dfrac{{343}}{6}y - \dfrac{2}{5}{y^{\dfrac{5}{2}}} + \dfrac{{{y^3}}}{{18}} - \dfrac{7}{{12}}{y^2}} \right]_1^{49} \\\ \Rightarrow V = 4\pi \left[ {\dfrac{{98}}{3} - \dfrac{2}{5}} \right] + 2\pi \left[ {\dfrac{{98}}{3} \times 343 - \dfrac{{49}}{6}.\dfrac{{2401}}{2} + \dfrac{{343}}{6} \times 49 - \dfrac{2}{5} \times 16807 + \dfrac{{117649}}{{18}} - \dfrac{7}{{12}} \times 2401 - \dfrac{{98}}{3} + \dfrac{{49}}{{12}} - \dfrac{{343}}{6} + \dfrac{2}{5} - \dfrac{1}{{18}} + \dfrac{7}{{12}}} \right] \\\ \Rightarrow V = 4\pi \left[ {\dfrac{{490 - 6}}{{15}}} \right] + 2\pi \left[ {\dfrac{{33614}}{3} - \dfrac{{117649}}{{12}} + \dfrac{{16807}}{6} - \dfrac{{33614}}{5} + \dfrac{{117649}}{{18}} - \dfrac{{16807}}{{12}} - \dfrac{{98}}{3} + \dfrac{{49}}{{12}} - \dfrac{{343}}{6} + \dfrac{2}{5} - \dfrac{1}{{18}} + \dfrac{7}{{12}}} \right] \\\ \Rightarrow V = \dfrac{{1936\pi }}{{15}} + 2\pi \left[ {\dfrac{{134456 - 117649 - 16807 - 392 + 49 + 7}}{{12}} + \dfrac{{50421 + 117649 - 1029 - 1}}{{18}} + \dfrac{{2 - 33614}}{5}} \right] \\\ \Rightarrow V = \dfrac{{1936\pi }}{{15}} + 2\pi \left[ {\dfrac{{ - 336}}{{12}} + \dfrac{{167040}}{{18}} + \dfrac{{ - 33612}}{5}} \right] = \dfrac{{1936\pi }}{{15}} + 2\pi \left[ { - 28 + 9280 + \dfrac{{ - 33612}}{5}} \right] \\\ \Rightarrow V = \dfrac{{1936\pi }}{{15}} + 2\pi \left[ {\dfrac{{ - 140 + 46400 - 33612}}{5}} \right] = \dfrac{{1936\pi }}{{15}} + \dfrac{{25296\pi }}{5} = \dfrac{{77824\pi }}{{15}} \;$$

Hence the volume of the required solid is $\dfrac{{77824\pi }}{{15}}$.
So, the correct answer is “ $\dfrac{{77824\pi }}{{15}}$ cc.”.

Note : In the shell method we assumed the solid figure to be the sum of infinitesimal vertical cylinders. For the vertical cylinders the integral is changed in the form of $y$ . We have to draw the graph and observe the critical points to put the limits according to the function that represents the solid in that range.