Question

How do you use the reference angles to find $\sin {210^ \circ }\cos {330^ \circ } - \tan {135^ \circ }$?

Answer 1

To simplify $\sin {210^ \circ }\cos {330^ \circ } - \tan {135^ \circ }$ using the reference angle, we will find the value of given angles step by step. Using the concept of reference angle, we will write
$\sin {210^ \circ } = \sin ({180^ \circ } + {30^ \circ })$,
$\cos {330^ \circ } = \cos \left( {{{360}^ \circ } - {{30}^ \circ }} \right)$ and
$\tan {135^ \circ } = \tan \left( {{{180}^ \circ } - {{45}^ \circ }} \right)$.
Then using the value of standard angles, we will find the value of $\sin {210^ \circ }\cos {330^ \circ } - \tan {135^ \circ }$.

Complete step by step answer:
According to the question, using the reference angles we have to find the value of $\sin {210^ \circ }\cos {330^ \circ } - \tan {135^ \circ }$. As we know, the reference angle is the acute angle with the x-axis. Thus, one by one we have to find the value of $\sin {210^ \circ }$, $\cos {330^ \circ }$ and $\tan {135^ \circ }$ using the reference angle.
Let us consider the original angle given by $\theta$ and the auxiliary value is given by $\alpha$.
For the first quadrant, we have $\theta = \alpha$.
For the second quadrant, we have $\theta = {180^ \circ } - \alpha$.
For the third quadrant, we have $\theta = {180^ \circ } + \alpha$.
For the fourth quadrant, we have $\theta = {360^ \circ } - \alpha$.

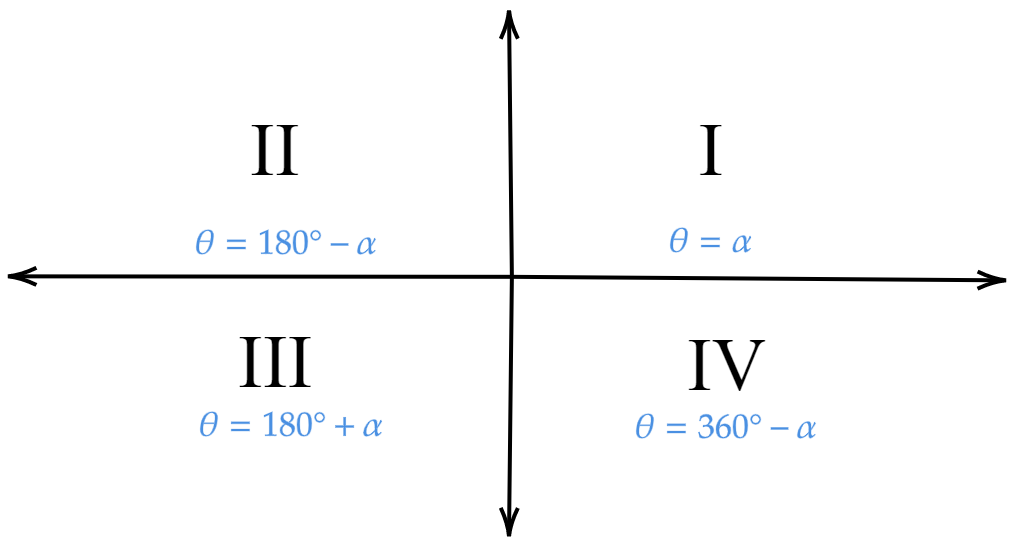
Consider $\sin {210^ \circ }$. ${210^ \circ }$ is in the third quadrant.
Therefore, $\sin {210^ \circ } = \sin ({180^ \circ } + \alpha )$ i.e., $\sin {210^ \circ } = \sin ({180^ \circ } + {30^ \circ })$
In the third quadrant, $\sin$ is negative.
So,
$\Rightarrow \sin ({180^ \circ } + {30^ \circ }) = - \sin {30^ \circ }$
$\therefore \sin ({210^ \circ }) = - \dfrac{1}{2}$
Now, consider $\cos {330^ \circ }$. ${330^ \circ }$ lies in the fourth quadrant.
Therefore, $\cos {330^ \circ } = \cos \left( {{{360}^ \circ } - {{30}^ \circ }} \right)$.
In the fourth quadrant, $\cos$ is positive.
So,
$\Rightarrow \cos \left( {{{360}^ \circ } - {{30}^ \circ }} \right) = \cos {30^ \circ }$
$\therefore \cos \left( {{{330}^ \circ }} \right) = \dfrac{{\sqrt 3 }}{2}$
Now, consider $\tan {135^ \circ }$. ${135^ \circ }$ lies in the second quadrant.
Therefore, $\tan {135^ \circ } = \tan \left( {{{180}^ \circ } - {{45}^ \circ }} \right)$.
In the second quadrant, $\tan$ is negative.
So,
$\Rightarrow \tan \left( {{{180}^ \circ } - {{45}^ \circ }} \right) = - \tan {45^ \circ }$
$\therefore \tan {135^ \circ } = - 1$
Putting the values in $\sin {210^ \circ }\cos {330^ \circ } - \tan {135^ \circ }$, we get
$\Rightarrow \sin {210^ \circ }\cos {330^ \circ } - \tan {135^ \circ } = \left( { - \dfrac{1}{2}} \right)\left( {\dfrac{{\sqrt 3 }}{2}} \right) - \left( { - 1} \right)$
On simplifying, we get
$\Rightarrow \sin {210^ \circ }\cos {330^ \circ } - \tan {135^ \circ } = 1 - \dfrac{{\sqrt 3 }}{4}$
Therefore, the value of $\sin {210^ \circ }\cos {330^ \circ } - \tan {135^ \circ }$ is $\left( {1 - \dfrac{{\sqrt 3 }}{4}} \right)$.

Note:
In the first quadrant, all trigonometric functions are positive. In the second quadrant, $\sin$ and $\cos ec$ are positive. In the third quadrant, $\tan$ and $\cot$ are positive. In the fourth quadrant, $\cos$ and $\sec$ are positive. Also, note that here we have used values of some standard angles i.e., $\sin {30^ \circ } = \dfrac{1}{2}$, $\cos {30^ \circ } = \dfrac{{\sqrt 3 }}{2}$ and $\tan {45^ \circ } = 1$.