Question

How do you use the quadratic formula to solve $12{\sin ^2}x - 13\sin x + 3 = 0$ in the interval $\left[ {0,2\pi } \right)$?

Answer 1

First, substitute $u$ for all occurrences of $\sin x$ and find the value of $u$ using quadratic formula. Then, compare the given quadratic equation to the standard quadratic equation and find the value of numbers $a$, $b$ and $c$ in the given equation. Then, substitute the values of $a$, $b$ and $c$ in the formula of discriminant and find the discriminant of the given equation. Finally, put the values of $a$, $b$ and $D$ in the roots of the quadratic equation formula. Next, replace all occurrences of $u$ with $\sin x$ solve for $x$ using trigonometric properties. Then, we will get all solutions of the given equation in the given interval.

Formula used:
The quantity $D = {b^2} - 4ac$ is known as the discriminant of the equation $a{x^2} + bx + c = 0$ and its roots are given by
$x = \dfrac{{ - b \pm \sqrt D }}{{2a}}$ or $x = \dfrac{{ - b \pm \sqrt {{b^2} - 4ac} }}{{2a}}$

Complete step by step solution:
Given equation: $12{\sin ^2}x - 13\sin x + 3 = 0$
We have to find all possible values of $x$ satisfying a given equation in the interval $\left[ {0,2\pi } \right)$.
So, first put $u = \sin x$, i.e., substitute $u$ for all occurrences of $\sin x$.
$\Rightarrow 12{u^2} - 13u + 3 = 0$
Now, we have to find the value of $u$ using a quadratic formula.
We know that an equation of the form $a{x^2} + bx + c = 0$, $a,b,c,x \in R$, is called a Real Quadratic Equation.
The numbers $a$, $b$ and $c$ are called the coefficients of the equation.
The quantity $D = {b^2} - 4ac$ is known as the discriminant of the equation $a{x^2} + bx + c = 0$ and its roots are given by
$x = \dfrac{{ - b \pm \sqrt D }}{{2a}}$ or $x = \dfrac{{ - b \pm \sqrt {{b^2} - 4ac} }}{{2a}}$
First, compare $3{x^2} + 5x = 0$ quadratic equation to standard quadratic equation and find the value of numbers $a$, $b$ and $c$.
Comparing $12{u^2} - 13u + 3 = 0$ with $a{x^2} + bx + c = 0$, we get
$a = 12$, $b = - 13$ and $c = 3$
Now, substitute the values of $a$, $b$ and $c$ in $D = {b^2} - 4ac$ and find the discriminant of the given equation.
$D = {\left( { - 13} \right)^2} - 4\left( {12} \right)\left( 3 \right)$
After simplifying the result, we get
$\Rightarrow D = 169 - 144$
$\Rightarrow D = 25$
Which means the given equation has real roots.
Now putting the values of $a$, $b$ and $D$ in $u = \dfrac{{ - b \pm \sqrt D }}{{2a}}$, we get
$u = \dfrac{{ - \left( { - 13} \right) \pm 5}}{{2 \times 12}}$
It can be written as
$\Rightarrow u = \dfrac{{13 \pm 5}}{{24}}$
$\Rightarrow u = \dfrac{3}{4}$ and $u = \dfrac{1}{3}$
Now, replace all occurrences of $u$ with $\sin x$.
$\Rightarrow \sin x = \dfrac{3}{4}$ and $\sin x = \dfrac{1}{3}$
First, we will find the values of $x$ satisfying $\sin x = \dfrac{3}{4}$.
So, take the inverse sine of both sides of the equation to extract $x$ from inside the sine.
$x = \arcsin \left( {\dfrac{3}{4}} \right)$
Since, the exact value of $\arcsin \left( {\dfrac{3}{4}} \right) = 0.848062079$.
$\Rightarrow x = 0.848062079$
Since, the sine function is positive in the first and second quadrants.
So, to find the second solution, subtract the reference angle from $\pi$ to find the solution in the second quadrant.
$x = 3.14 - 0.848062079$
$\Rightarrow x = 2.293530575$
Since, the period of the $\sin x$ function is $2\pi$ so values will repeat every $2\pi$ radians in both directions.
$x = 0.848062079 + 2n\pi ,2.293530575 + 2n\pi$, for any integer $n$.
First, we will find the values of $x$ satisfying $\sin x = \dfrac{1}{3}$.
So, take the inverse sine of both sides of the equation to extract $x$ from inside the sine.
$x = \arcsin \left( {\dfrac{1}{3}} \right)$
Since, the exact value of $\arcsin \left( {\dfrac{1}{3}} \right) = 0.3398369095$.
$\Rightarrow x = 0.3398369095$
Since, the sine function is positive in the first and second quadrants.
So, to find the second solution, subtract the reference angle from $\pi$ to find the solution in the second quadrant.
$x = 3.14 - 0.3398369095$
$\Rightarrow x = 2.801755744$
Since, the period of the $\sin x$ function is $2\pi$ so values will repeat every $2\pi$ radians in both directions.
$x = 0.3398369095 + 2n\pi ,2.801755744 + 2n\pi$, for any integer $n$.
Thus, $x = 0.848062079 + 2n\pi ,2.293530575 + 2n\pi ,0.3398369095 + 2n\pi ,2.801755744 + 2n\pi$
Where, $n$ is any integer, i.e., $n = 0, \pm 1, \pm 2, \pm 3,......$
Now, find all values of $x$ in the interval $\left[ {0,2\pi } \right)$.
Since, it is given that $x \in \left[ {0,2\pi } \right)$, hence put $n = 0$ in the general solution.
So, putting $n = 0$ in the general solution, $x = 0.848062079 + 2n\pi ,2.293530575 + 2n\pi ,0.3398369095 + 2n\pi ,2.801755744 + 2n\pi$, we get
$\therefore x = 0.848062079,2.293530575,0.3398369095,2.801755744$
Final solution: Hence, $x = 0.848062079,2.293530575,0.3398369095,2.801755744$ are the solutions of the given equation in the given interval.

Note:
In above question, we can find the solutions of given equation by plotting the equation, $12{\sin ^2}x - 13\sin x + 3 = 0$ on graph paper and determine all solutions which lie in the interval, $\left[ {0,2\pi } \right)$.

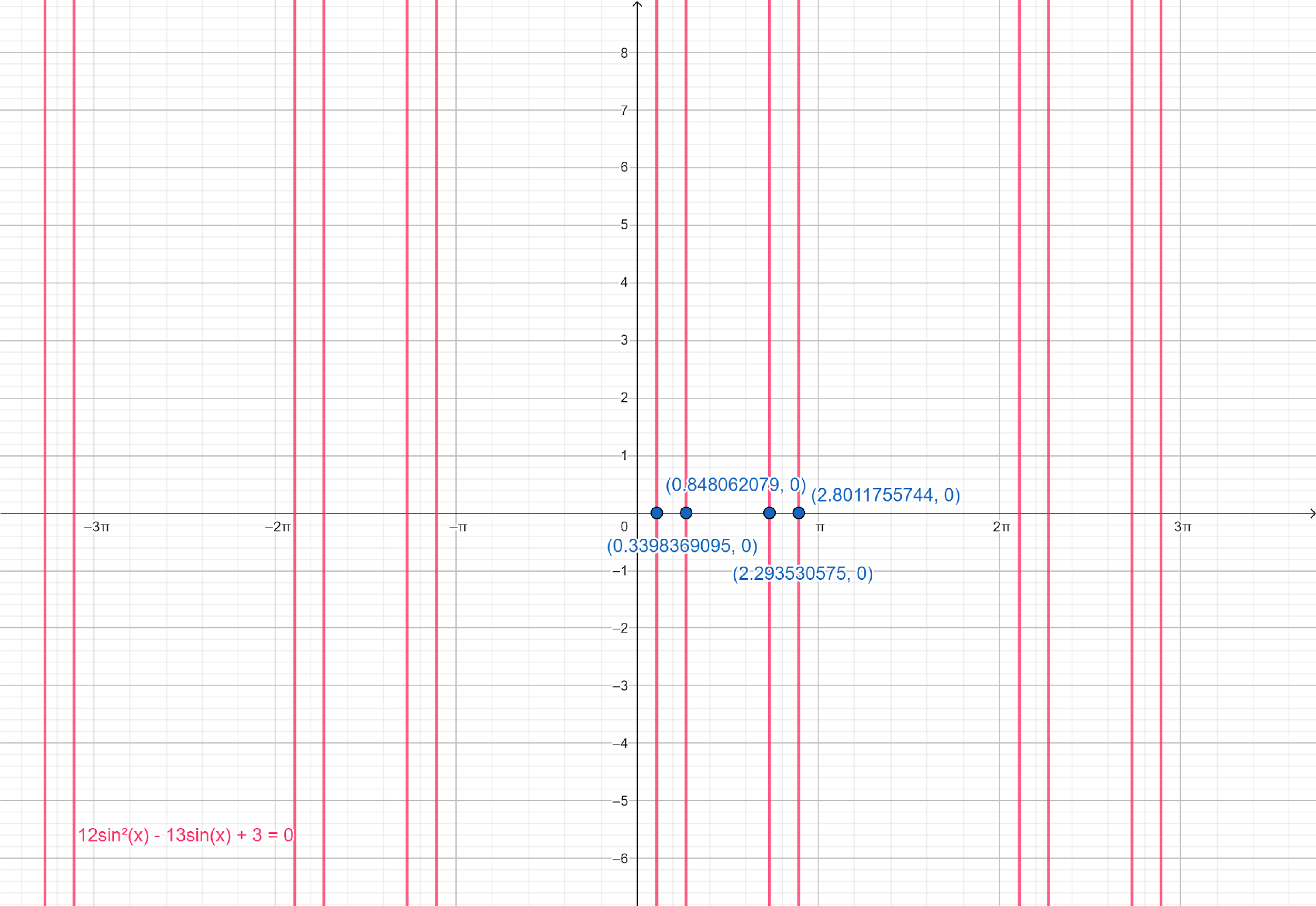
From the graph paper, we can see that there are four values of $x$ in the interval $\left[ {0,2\pi } \right)$.
So, these will be the solutions of the given equation in the given interval.
Final solution: Hence, $x = 0.848062079,2.293530575,0.3398369095,2.801755744$ are the solutions of the given equation in the given interval.