Question

How do you use the Pythagorean theorem to find the distance between the points (3,0) and (-3,6)?

Answer 1

Hint : Here to solve the given question we need to use the Pythagorean Theorem which says, square of sum of base and height for a right angle triangle is equal to the square of length of hypotenuse of that triangle, for using that here first we need to get the triangle formed by theses points.
Formulae Used: Pythagorean theorem
$\Rightarrow A{B^2} + B{C^2} = A{C^2}$

Complete step by step solution:
In order to get the triangle formed by these points, first we need to see the point’s coordinates, and then draw perpendicular lines to the axis so as to get the triangle, on solving we get:

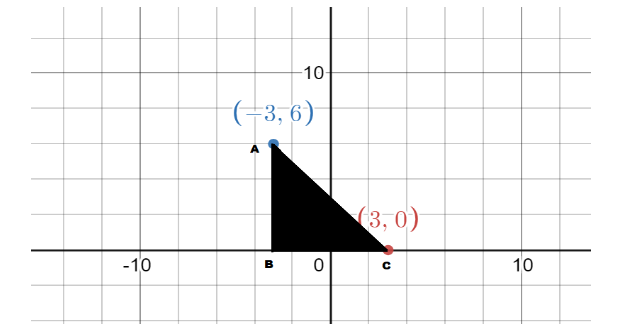
Here we get the required triangle in the upper figure drawn, now we have to use the Pythagorean theorem for the triangle ABC in the figure to get the side length AC, here we know that length of side AB is six unit, and the length of side BC is three unit, by the coordinates of theses points, now on solving we get:

$$\Rightarrow A{B^2} + B{C^2} = A{C^2} \\\ \Rightarrow {(6)^2} + {(6)^2} = A{C^2} \\\ \Rightarrow A{C^2} = 36 + 36 = 72 \\\ \Rightarrow AC = \sqrt {72} = 8.49 \;$$

Here we got the length of the required side asked in the question.
So, the correct answer is “$AC = \sqrt {45} = 8.49 Units$”.

Note : The given question need to be first plotted on the graph in order to obtain the triangle, so that the given theorem can be used, if the theorem was not mandatory, then for finding the length between two points, we can directly use the line segment formulae and get the desired length.