Question

How do you use the method of linear interpolation to approximate values and create an equation of a line?

Answer 1

In this question we have been asked to explain how we use the method of linear interpolation to approximate values and create an equation of a line. For answering this question we will assume two points $A(0,5)$ and $B\left( -2.5,0 \right)$ , try to find the equation of the straight line passing through these points.

Complete step by step solution:
Now considering from the question we have been asked to explain how we use the method of linear interpolation to approximate values and create an equation of a line.
For answering this question we will assume two points $A(0,5)$ and $B\left( -2.5,0 \right)$ , try to find the equation of the straight line passing through these points.
From the basic concepts of lines we know that the general equation of a straight line is given as $y=mx+c$ where $m$ is the slope of the straight line.
From the basic concepts we know that the slope of the straight line passing through points $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$ is given as $\Rightarrow \dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}$ .
Now we will try to find the slope of the assumed straight line passing through these points.
The slope of this line is given as
$\begin{aligned} & \Rightarrow \dfrac{0-5}{-2.5-0}=\dfrac{-5}{-2.5} \\\ & \Rightarrow \dfrac{5\times 10}{25}=2 \\\ \end{aligned}$.
Now we have got some part of the equation which is given as $y=2x+c$ .
Now we need to find the value of $c$ for that we will substitute any one point in this equation. By doing this using the point $\left( 0,5 \right)$ we will have
$\begin{aligned} & 5=0+c \\\ & \Rightarrow c=5 \\\ \end{aligned}$
Now we can say that the line equation passing through these two points $A(0,5)$ and $B\left( -2.5,0 \right)$ is given as $y=2x+5$ .
The graph of this equation will look like:

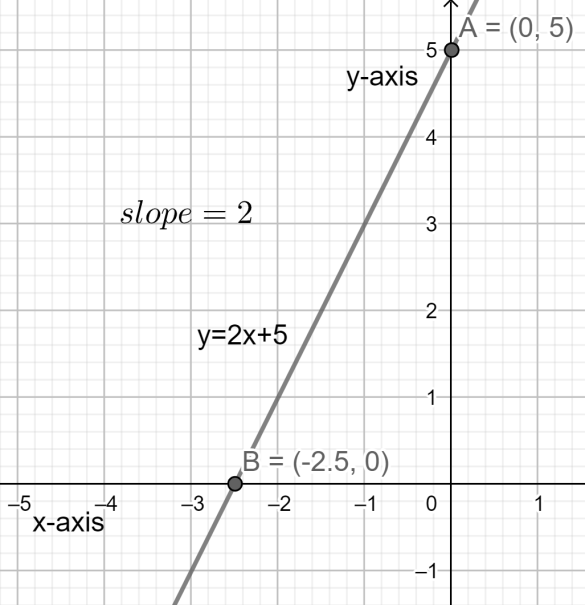
Therefore we can conclude that we can use the method of linear interpolation to approximate values and create an equation of a line similarly. Similarly we can find any line equation passing through any points.

Note: During the process of answering questions of this type we should be sure with our concepts that we apply. Similarly we can find the equation of line passing through $\left( 3,0 \right)$ and $\left( 0,6 \right)$ which will be given as $y=2x+6$ .