Question

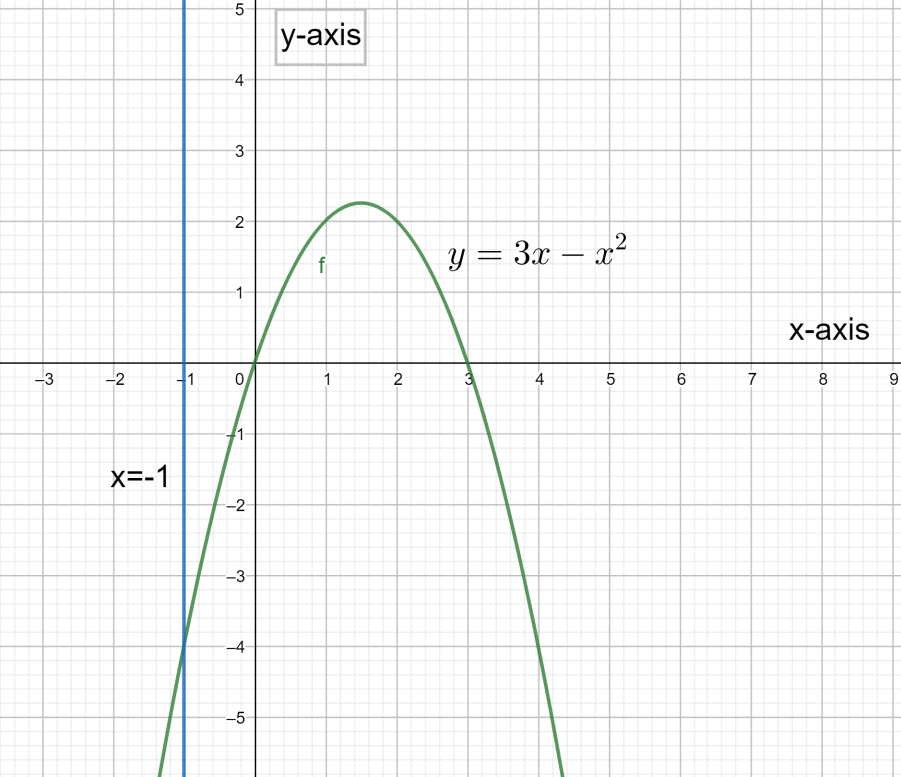
How do you use the method of cylindrical shells to find the volume of the solid obtained by rotating the region bounded by $y=f\left( x \right)=3x-{{x}^{2}}$ and x axis revolved about the $x=-1$?

Answer 1

From the question we have to find the volume of the solid obtained by rotating the region bounded by$y=f\left( x \right)=3x-{{x}^{2}}$ and x axis revolved about the $x=-1$ that to by using method of cylindrical shells. First, we have to Imagine a cylindrical shell as a rectangular prism with width $f\left( x \right)$, length $2\pi r$, and thickness $\delta x$. The reason for the length being $2\pi r$ is that if we unravel a cylindrical shell into a rectangular prism, the length corresponds to the circumference of the circular cross-section of the original cylinder. Then The volume of the cylindrical shell is $width\times length\times thickness\text{ }\left( height \right)$.

Complete step by step answer:
From the question given we have the width
The width is
$\Rightarrow width=f\left( x \right)=3x-{{x}^{2}}$
We have to Imagine a cylindrical shell as a rectangular prism with width $f\left( x \right)$, length $2\pi r$, and thickness $\delta x$.
Therefore, the volume will be
$\Rightarrow volume=2\pi r\times \left( 3x-{{x}^{2}} \right)\times \delta x$
If we sketch the parabola $y=3x-{{x}^{2}}$ we can see that the region bounded by this parabola and the x-axis resides in the domain $0\le x\le 3$.
Also, the radius of the cylindrical shell is considered to be the distance from the axis of revolution $x=-1$ and the edge of the shell (i.e., at a position x within the domain $0\le x\le 3$).
Hence,
$\Rightarrow r=1+x$
Therefore, the volume will be
$\Rightarrow volume=2\pi \left( 1+x \right)\times \left( 3x-{{x}^{2}} \right)\times \delta x$
That is the change in volume is,
$\Rightarrow \delta v=2\pi \left( 1+x \right)\times \left( 3x-{{x}^{2}} \right)\times \delta x$
To find the volume, we limit the thickness of the shells, and find their summation within the domain $0\le x\le 3$.
$\Rightarrow V=\displaystyle \lim_{\delta x \to 0}\sum\limits_{x=0}^{3}{2\pi \left( 1+x \right)\times \left( 3x-{{x}^{2}} \right)\times \delta x}$
$\Rightarrow V=2\pi \int\limits_{0}^{3}{\left( 1+x \right)\times \left( 3x-{{x}^{2}} \right)dx}$
$\Rightarrow V=2\pi \int\limits_{0}^{3}{\left( 3x+2{{x}^{2}}-{{x}^{3}} \right)dx}$
$\Rightarrow V=2\pi \mathop{\left[ \dfrac{3}{2}{{x}^{2}}+\dfrac{2}{3}{{x}^{3}}-\dfrac{1}{4}{{x}^{4}} \right]}_{0}^{3}$
$\Rightarrow V=2\pi \left[ \dfrac{45}{4} \right]$
$\Rightarrow V=\dfrac{45\pi }{2}$
Therefore, the volume of the solid is $\dfrac{45\pi }{2}$

Note: Students should learn to draw the graphs for the given equation and the students should know how to apply the limits. Students should also know the integration part. Students should be very careful in doing the calculation part.