Question

How do you use the horizontal line test to determine whether the function $g\left( x \right)={{\left( x+5 \right)}^{3}}$ is one to one?

Answer 1

In the above mentioned question we have to check whether the given function is one to one or not through horizontal line test, for this we need to first understand the basic concept of what do we mean by horizontal line test and how can we apply it then we will be able to solve this question with ease.

Complete step-by-step solution:
In the above mentioned question we need to check whether the given function is one to one or not and the method to use is also specified as a horizontal line test. This test basically uses a straight horizontal line which is parallel to x-axis. For this test we need to first draw the graph of the equation and then draw a straight horizontal line if the line crosses the graph that has been drawn for the equation mentioned in the question more than once then the equation given is not one to one and if it does not then the equation can be regarded as one to one, this is what horizontal line test is. Now in our question first we are going to make the graph for the equation then draw a straight horizontal line and we will get it as

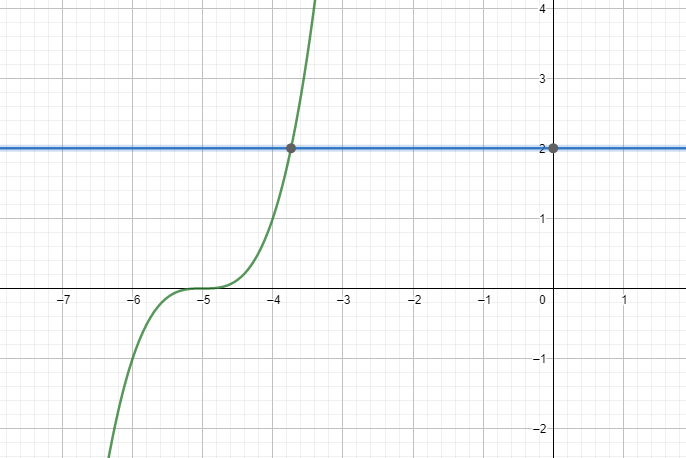
Now from the above graph we can see that the horizontal line cuts the graph only once so this can be considered as one to one equation.
The function that has been mentioned in the question is a one to one equation.

Note: In the above question you can draw the horizontal line at any place where the graph exists to check whether it holds true for one on one. This question can also be solved in another way as we can see that the power mentioned is not in even number so the equation will not have two values of y for both positive and negative values of x if the power is odd the number in the brackets will be positive if the number is positive and negative if the number is negative and also as the number is not a modulus function or have even power the function will be one to one generally except for some cases.