Question

How do you use the graph of $f\left( x \right) = \sec x$ to determine whether the function is even, odd or neither?

Answer 1

Given a trigonometric function. We have to find out whether the function is even, odd or neither using the graph of the function. First, draw the graph of the function $f\left( x \right) = \sec x$. Then, we have to draw the graph of the function, $f\left( { - x} \right)$by substituting $x = - x$ into the function $f\left( x \right) = \sec x$. Then, determine whether the function is even, odd or neither. The function is even if the value of $f\left( { - x} \right)$is equal to the function itself, for all values of x. The function is defined as an odd function if $f\left( { - x} \right)$is equal to $- f\left( x \right)$, for all values of x.

Complete step by step solution:
We are given the expression $f\left( x \right) = \sec x$. First, we will draw the graph of the function.

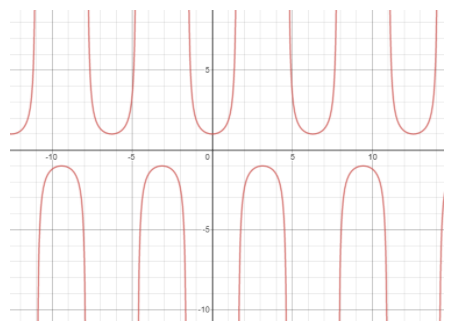
Now, we will substitute $x = - x$ into the function.
$\Rightarrow f\left( { - x} \right) = \sec \left( { - x} \right)$
On applying the trigonometric property, we get:
$\Rightarrow f\left( { - x} \right) = \sec \left( x \right)$
Now, the graph of the function $f\left( { - x} \right)$ is shown below:

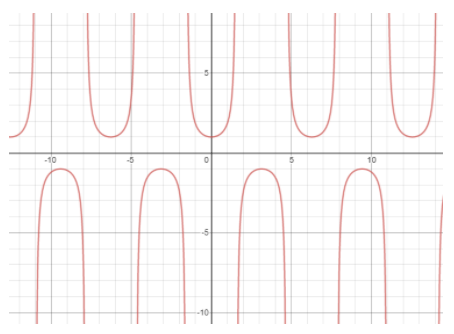
From the graph, it is observed that the graph is symmetric with respect to the y-axis which means the function is an even function.

Final answer: Hence, the function $f\left( x \right) = \sec x$ is an even function.

Note:
The students must remember that the functions which are symmetrical about the y-axis are even functions whereas if the graph of the function is symmetric about the origin, then the function is an odd function. Students must also note that we have used trigonometric identities and properties such as:
$\Rightarrow \cos \left( { - x} \right) = \cos x$
$\Rightarrow \sec \left( { - x} \right) = \sec x$
$\Rightarrow \sin \left( { - x} \right) = - \sin x$
$\Rightarrow \tan \left( { - x} \right) = - \tan x$
$\Rightarrow \csc \left( { - x} \right) = - \csc x$
$\Rightarrow \cot \left( { - x} \right) = - \cot x$

In the trigonometric identities where the equation $f\left( { - x} \right) = f\left( x \right)$ holds, the trigonometric identities are even otherwise the functions are odd functions. Therefore, cosine and secant functions are even functions and the sine, tangent, cosecant and cotangent functions are odd functions.