Question

How do you use the first and second derivatives to sketch y = 3{x^4} - 4{x^3}$$$$?

Answer 1

First find the first derivative of the given function and equate it to zero to find the critical points of the given function. Then find the second order derivative using that find the maximum and minimum values of the given function and also find the points of inflection by equating the second order derivative to zero. Using the above points draw the graph of the given function.

Complete step by step solution:
Given $f(x) = y = 3{x^4} - 4{x^3}$---(1)
Differentiating with respect to $x$ both sides of the equation (1), we get
$\dfrac{{dy}}{{dx}} = 12{x^3} - 12{x^2}$--(2)
Equating the equation (2) to zero to find the critical points, we get

$$\Rightarrow 12{x^3} - 12{x^2} = 0 \\\ \Rightarrow x = 0,1 \\\$$

Hence, the critical values are $x = 0$ and $x = 1$.
then $f(0) = 0$,$f(1) = 3 - 4 = - 1$
Hence, the critical points are $\left( {0,0} \right)$ and $\left( {1, - 1} \right)$.
Differentiating with respect to $x$ both sides of the equation (2), we get
${f^{''}}(x) = \dfrac{{{d^2}y}}{{d{x^2}}} = 36{x^2} - 24x$--(3)
At $x = 0\;$, ${f^{''}}(0) = 0$ and at $\;x = 1$, ${f^{''}}(1) = 12 > 0$
We use the first derivative test to find out if this point is a relative minimum, maximum and inflection.
At $\left( {1, - 1} \right)$, $f(x)$ has relative minima.
To find inflection points let ${f^{''}}(x) = 0$ in the equation (3), we get

$$\Rightarrow x = 0,\dfrac{2}{3} \\\$$

Inflections at $x = 0\;$,$f(0) = 0$ and at x = \dfrac{2}{3}$$$$f\left( {\dfrac{2}{3}} \right) = 3{\left( {\dfrac{2}{3}} \right)^4} - 4{\left( {\dfrac{2}{3}} \right)^3} = - \dfrac{{16}}{{27}}
Inflection points $\left( {0,0} \right)$,$\left( {\dfrac{2}{3}, - \dfrac{{16}}{{27}}} \right)$.
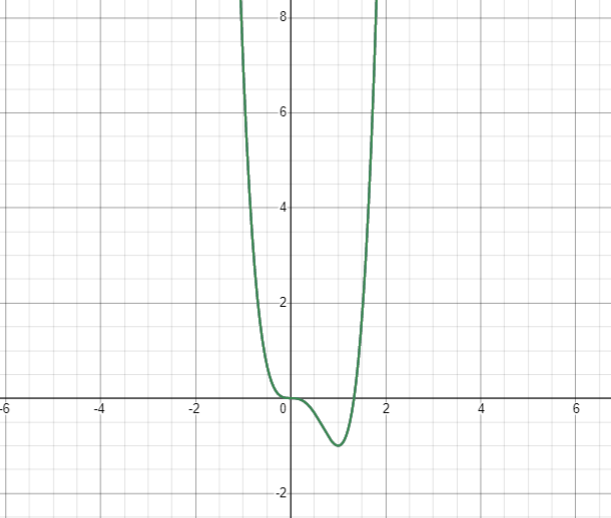
Since fourth order functions have end conditions both positive. Put a point at $\left( {0,0} \right)$ and a point at the relative minimum $\left( {1, - 1} \right)$. Start at the upper left and create a horizontal inflection at $\left( {0,0} \right)$, then turn downward to the relative minimum, then curve upward.
The graph of the given function:

Note:
Note that a function is continuous if you can draw its graph without lifting the pencil. A function is said to be differentiable if it has no shape edge (cusp) in the graph of each derivative. Every differentiable function is continuous but the converse is not true.