Question

How do you use the first and second derivative to sketch $F(x) = \dfrac{{\ln (x)}}{{\sqrt x }}$ ?

Answer 1

Hint : In this question we are asked to use the first and second derivative of the function. In order to proceed with this question we need to know what differentiation is. Differentiation is a way to find the instantaneous change of rate in function which depends on one of its variables. The example which we can commonly see is Velocity, which is the rate change of displacement with respect to time. Anti-differentiation is the opposite of finding a derivative. If x and y are two variables in an expression, then the rate of change of x with respect to y can be denoted by dy/dx. The expression which we write in general for derivatives of a function can be represented as f'(x) = dy/dx, where y = f(x) is any function.

Complete step by step solution:
We are given,
$F(x) = \dfrac{{\ln (x)}}{{\sqrt x }}$
We’ll apply quotient rules to differentiate the given expression.
First derivative-
$\dfrac{d}{{dx}}[\dfrac{{f(x)}}{{g(x)}}] = \dfrac{{g(x)f'(x) - f(x)g'(x)}}{{{{[g(x)]}^2}}}$
$\Rightarrow f(x) = \ln (x) \\\ \Rightarrow g(x) = \sqrt x \\\$
$\Rightarrow f'(x) = \dfrac{1}{x} \\\ \Rightarrow g'(x) = \dfrac{1}{2} \times \dfrac{1}{{\sqrt x }} \;$
$\Rightarrow \dfrac{d}{{dx}}[\dfrac{{\ln (x)}}{{\sqrt x }}] = \dfrac{{\sqrt x \times \dfrac{1}{x} - \ln (x) \times \dfrac{1}{2} \times \dfrac{1}{{\sqrt x }}}}{{{{(\sqrt x )}^2}}}$
$\Rightarrow \dfrac{d}{{dx}}[\dfrac{{\ln (x)}}{{\sqrt x }}] = \dfrac{{\dfrac{{\sqrt x }}{x} - \dfrac{{\ln (x)}}{{2\sqrt x }}}}{x}$
$\Rightarrow \dfrac{d}{{dx}}[\dfrac{{\ln (x)}}{{\sqrt x }}] = \dfrac{{\dfrac{1}{{\sqrt x }} - \dfrac{{\ln (x)}}{{2\sqrt x }}}}{x}$
$\Rightarrow \dfrac{d}{{dx}}[\dfrac{{\ln (x)}}{{\sqrt x }}] = \dfrac{{\dfrac{{2 - \ln (x)}}{{2\sqrt x }}}}{x}$
$\Rightarrow \dfrac{d}{{dx}}[\dfrac{{\ln (x)}}{{\sqrt x }}] = \dfrac{{2 - \ln (x)}}{{2x\sqrt x }}$
To find the critical points-
$\Rightarrow \dfrac{{2 - \ln (x)}}{{2x\sqrt x }} = 0$
$\Rightarrow 2 - \ln (x) = 0$
$\Rightarrow \ln (x) = 2$
$\Rightarrow {e^{\ln (x)}} = {e^2}$
$\Rightarrow x = {e^2}$
By putting the value in the function
$\Rightarrow F({e^2}) = \dfrac{{\ln ({e^2})}}{{\sqrt {{e^2}} }}$
$\Rightarrow F({e^2}) = \dfrac{2}{e}$
So the turning point of the graph is at $({e^2},\dfrac{2}{e})$
When
$\Rightarrow 0 < x < {e^2}$
$\Rightarrow f'(x) > 0$
$\Rightarrow {e^2} < x$
$\Rightarrow f'(x) < 0$
Second Derivative
$\Rightarrow f(x) = 2 - \ln (x) \\\ \Rightarrow g(x) = 2x\sqrt x = 2{x^{\dfrac{3}{2}}} \\\$

$$\Rightarrow f'(x) = \dfrac{1}{x} \\\ \Rightarrow g'(x) = 2[\dfrac{3}{2}{x^{\dfrac{1}{2}}}] = 3{x^{\dfrac{1}{2}}} \;$$

$\Rightarrow \dfrac{{d'}}{{dx}}[\dfrac{{\ln (x)}}{{\sqrt x }}] = \dfrac{{2{x^{\dfrac{3}{2}}} \times \dfrac{1}{x} - [2 - \ln (x) \times 3{x^{\dfrac{1}{2}}}]}}{{{{(2{x^{\dfrac{3}{2}}})}^2}}}$
$\Rightarrow \dfrac{{d'}}{{dx}}[\dfrac{{\ln (x)}}{{\sqrt x }}] = \dfrac{{2{x^{\dfrac{1}{2}}} - 6{x^{\dfrac{1}{2}}} + \ln (x) \times 3{x^{\dfrac{1}{2}}}]}}{{{{(2{x^{\dfrac{3}{2}}})}^2}}}$
$\Rightarrow \dfrac{{d'}}{{dx}}[\dfrac{{\ln (x)}}{{\sqrt x }}] = \dfrac{{ - 4{x^{\dfrac{1}{2}}} + 3{x^{\dfrac{1}{2}}}\ln (x)]}}{{4{x^3}}}$
Since $f\prime \prime (x) > 0\;$ for all x in the domain, the function will extend till infiniti.
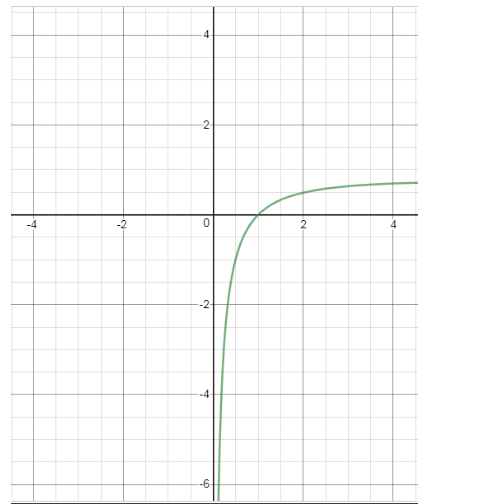
The function is negative for $0 < x < 1\;$ and positive for $x > 1$ .

Note : The basic differentiation rules that are followed while finding a derivative are as follows:
Sum and Difference Rule-
Product Rule
Quotient Rule
Chain Rule
Some applications of
Acceleration: The rate of change of velocity with respect to time
We use the derivative function to calculate the highest point and lowest point of the curve in a graph or to know its turning point.
The derivative function is used to find tangent and normal to a curve