Question

How do you use the epsilon delta definition to find the limit of $\left( {\dfrac{{{x^2} + x - 6}}{{x - 2}}} \right)$as $x$ approaches 2$$$$?

Answer 1

Here we have to check that the given function is defined or not at $x = 2$. If it is defined, then by the definition epsilon delta finds the relationship between epsilon and delta to prove the limit of the given function as $x$approaches to $2$ it exists and is unique.

Complete step by step solution:
The epsilon-delta definition of limits says that the limit of $f(x)$at $x = c$is $L$ if for any $\varepsilon > 0$ there exists a $\delta > 0$ such that if the distance of $x$ from $c$ is less than $\delta$, then the distance of f(x) from $L$ is less than $\varepsilon$.
Graphical representation of the epsilon-delta definition:

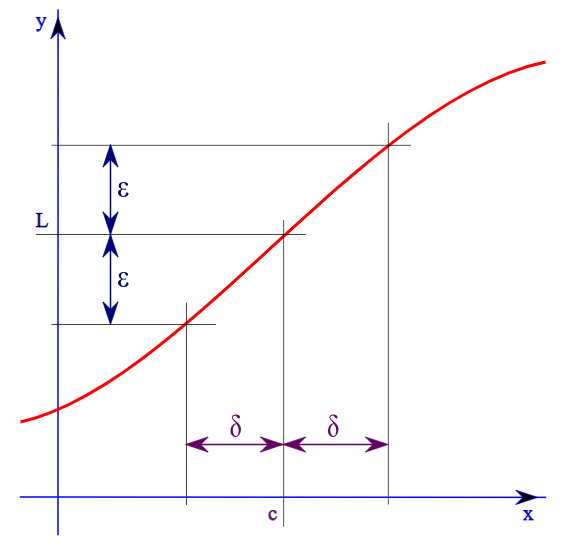
Let the given function say $f(x) = \left( {\dfrac{{{x^2} + x - 6}}{{x - 2}}} \right)$ and $L$ be the limit of the given function.
At $x = 2$, the given function approaches infinity. So, rewriting the given above function, we get $f(x) = x + 3$. Hence at $x = 2$,$f(2) = 5$.
$\Rightarrow$ $\mathop {\lim }\limits_{x \to 2} \left( {\dfrac{{{x^2} + x - 6}}{{x - 2}}} \right) = 5$
We prove by the epsilon delta definition, for any $\varepsilon > 0$ there exists a $\delta > 0$ such that
If $\left| {x - 2} \right| < \delta$ $\Rightarrow$ $\left| {f(x) - L} \right| < \varepsilon$
$\Rightarrow \left| {x + 3 - 5} \right| < \varepsilon$
On simplification,
$\Rightarrow \left| {x + 2} \right| < \varepsilon$
$\Rightarrow \left| {x + 2} \right| < \delta$
From the above two equations, we can say
$\delta = \varepsilon$
Hence the limit of $\left( {\dfrac{{{x^2} + x - 6}}{{x - 2}}} \right)$as $x$ approaches $2$ is $5$.

Note:
Note that If the limit of the given function at the given point exists then the limit is unique and finite. A function is continuous if you can draw its graph without lifting the pencil. Every differentiable function is continuous but converse is not true.