Question

How do you use the amplitude and the period to graph $y = \sin \left( {x + \dfrac{\pi }{2}} \right)$ ?

Answer 1

Hint : First, using the suitable trigonometric identities, simplify the given equation and try to get a simplest form of the equation so that we can understand it better. Then find the maximum value of the function and the interval after which the graph of the function starts repeating itself as the amplitude of the function is the maximum value of the function and period is the regular interval after which the graph repeats itself.

Complete step-by-step answer :
The given equation is $y = \sin \left( {x + \dfrac{\pi }{2}} \right) - - - - - - - - - \left( 1 \right)$
This is a trigonometric function. All trigonometric functions are periodic. This means that the function repeats itself after a regular interval on the Cartesian plane.
The trigonometric function $\sin x$ has a period of $2\pi$ radians. This means that the values of the function $\sin x$ repeat after every interval of $2\pi$ radians.
This helps in graphing the curve of a trigonometric function. We can graph the function for an interval of $2\pi$ radians and then just replicate the function for every such successive interval.
Let us simplify equation $1$ by using the identity $\sin \left( {\dfrac{\pi }{2} + \theta } \right) = \cos \theta$ .
Then,
$\Rightarrow y = \sin \left( {x + \dfrac{\pi }{2}} \right)$
$\Rightarrow y = \cos x$
So, we get, $y = \sin \left( {x + \dfrac{\pi }{2}} \right) = \cos x$
This means that the graph of equation $\left( 1 \right)$ is the same as the graph of trigonometric function $\cos x$ .
Now, we know that the amplitude of $\cos x$ is $1$ and the period of $\cos x$ is $2\pi$ . So, the amplitude of the function $y = \sin \left( {x + \dfrac{\pi }{2}} \right) = \cos x$ is $1$ which means that the maximum value of the function is $1$ and the period of the function $y = \sin \left( {x + \dfrac{\pi }{2}} \right) = \cos x$ is $2\pi$ radians which means that the graph repeats itself after an interval of $2\pi$ radians.
So, we get the graph of $y = \sin \left( {x + \dfrac{\pi }{2}} \right)$ as

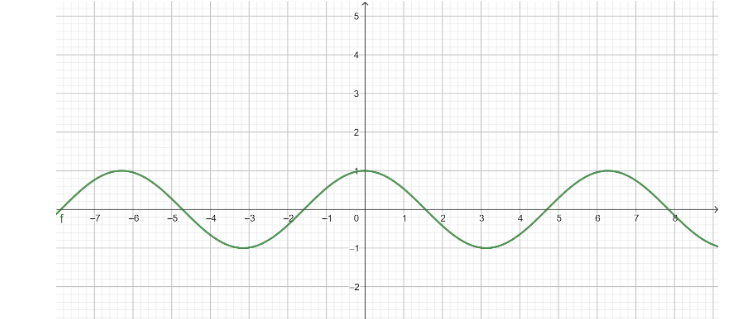
Note : If we have an equation $A\sin \left( {kx - \phi } \right)$ , then A is the amplitude, $\dfrac{{2\pi }}{k}$ is the period and $\phi$ is the phase shift of the graph.
Here, in this case, $A = 1$ , $k = 1$ and $\phi = - \dfrac{\pi }{2}$ .
This means that amplitude of the function is $1$ and period is $2\pi$ .