Question

How do you use end behaviour, zeroes, y intercepts to sketch the graph of $f\left( x \right)=\left( x-4 \right)\left( x-1 \right)\left( x+3 \right)$ ?

Answer 1

Hint : We first find the intercepts of the given function $f\left( x \right)=\left( x-4 \right)\left( x-1 \right)\left( x+3 \right)$ which also gives us the roots of the function. Then we use the differentiation to find the extremum points of the function and draw the graph.

Complete step-by-step answer :
We need to find the zeros, y intercepts of the curve $f\left( x \right)=\left( x-4 \right)\left( x-1 \right)\left( x+3 \right)$ .
Here the zeroes mean the x intercepts or the roots of the polynomial.
We put the value of $f\left( x \right)=0$ and get $\left( x-4 \right)\left( x-1 \right)\left( x+3 \right)=0$ which gives the roots as
$x=-3,1,4$ . The points are $\left( -3,0 \right),\left( 1,0 \right),\left( 4,0 \right)$ .
To find the y intercepts we put the value of $x=0$ and get $f\left( x \right)=\left( 0-4 \right)\left( 0-1 \right)\left( 0+3 \right)=12$ which gives the value as the intersecting point of $\left( 0,12 \right)$ .
Therefore, to find the extremum points we have to find the first and second order derivatives.
Extremum points in a curve have slope value 0.
The slope of the function $f\left( x \right)=\left( x-4 \right)\left( x-1 \right)\left( x+3 \right)$ can be found from the derivative of the function ${{f}^{'}}\left( x \right)=\dfrac{d}{dx}\left[ f\left( x \right) \right]$ .
We differentiate both sides of the function $f\left( x \right)=\left( x-4 \right)\left( x-1 \right)\left( x+3 \right)$ with respect to $x$ .
$\begin{aligned} & f\left( x \right)=\left( x-4 \right)\left( x-1 \right)\left( x+3 \right)={{x}^{3}}-2{{x}^{2}}-11x+12 \\\ & \Rightarrow {{f}^{'}}\left( x \right)=\dfrac{d}{dx}\left[ f\left( x \right) \right]=3{{x}^{2}}-4x-11 \\\ \end{aligned}$ .
To find the $x$ coordinates of the extremum point we take $3{{x}^{2}}-4x-11=0$ .
In the given equation we have $3{{x}^{2}}-4x-11=0$ . The values of $a,b,c$ is $3,-4,-11$ respectively.
We put the values and get $x$ as $x=\dfrac{4\pm \sqrt{{{4}^{2}}-4\times 3\times \left( -11 \right)}}{2\times 3}=\dfrac{4\pm \sqrt{148}}{6}=\dfrac{2\pm \sqrt{37}}{3}$ .
Therefore, from the value of the $x$ coordinates of the extremum points, we find their $y$ coordinates.
Therefore, the extremum points are $x=\dfrac{2\pm \sqrt{37}}{3}$ .

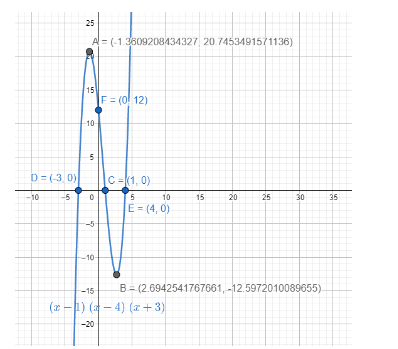
Note : We need to remember that the curve changes its direction on the extremum points only. Other that that the function $f\left( x \right)=\left( x-4 \right)\left( x-1 \right)\left( x+3 \right)$ is an increasing function in the range of $x\in \left[ 4,\infty \right)$ and decreasing function in the range of $x\in \left( -\infty ,-3 \right]$ .