Solveeit Logo
Login

Question

Question: How do you use \[\csc\ \theta = 5\] to find \[\sec(90^{o} - \theta)\] ?...

How do you use csc⁡ θ=5\csc\ \theta = 5 to find sec⁡(90o−θ)\sec(90^{o} - \theta) ?

Explanation

Solution

In this question, we need to find the value of sec⁡(90o−θ)\sec(90^{o} - \theta) with the use of csc⁡ θ=5\csc\ \theta = 5 . Sine , cosine and tangent functions are known as the basic trigonometric functions. Secant function is nothing but a ratio of hypotenuse of the right angle to the adjacent side of the right angle and also a reciprocal of the one of three basic functions. First, we need to consider a right angle triangle ABC, we need to find sec⁡(90o−θ)\sec(90^{o} - \theta) and cosec θ\text{cosec}\ \theta . Thus by equating and simplifying the expression, we can find the value of sec⁡(90o−θ)\sec(90^{o} - \theta).

Complete step by step answer:
Given, csc⁡ θ=5\csc\ \theta = 5. Here we need to find sec⁡(90o−θ)\sec(90^{o} - \theta). We know that secant function is the ratio of the hypotenuse side to the adjacent side.In the triangle, ABC,

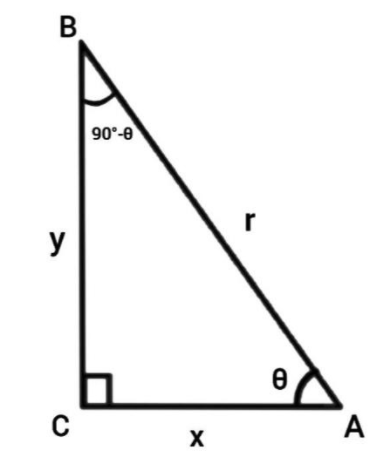
sec⁡ θ=hypotenuseadjacent side\sec\ \theta = \dfrac{\text{hypotenuse}}{\text{adjacent side}}
Here θ\theta is (90o−θ)(90^{o} - \theta)
sec⁡(90o−θ)=ry\sec(90^{o} - \theta) = \dfrac{r}{y} ••• (1)
Similarly we know that the Cosecant function is the ratio of the hypotenuse side to the opposite side.
Again in triangle ABC, when θ\theta is the angle,
cosec θ=hypotenuseopposite side\text{cosec}\ \theta = \dfrac{\text{hypotenuse}}{\text{opposite side}}
⇒cosec θ=ry\Rightarrow \text{cosec}\ \theta = \dfrac{r}{y} •••(2)
Thus on equating (1) and (2) ,
We get,
sec⁡(90o−θ) =cosec θ\sec(90^{o} - \theta)\ = \text{cosec}\ \theta
Given that cosec θ=5\text{cosec}\ \theta = 5
On substituting the cosecθ{\text{cosec}\theta} value,
We get,
sec⁡(90o−θ) =5\sec(90^{o} - \theta)\ = 5
Thus the value of sec⁡(90o−θ)\sec(90^{o} - \theta) is equal to 55

Therefore, the value of sec⁡(90o−θ)\sec(90^{o} - \theta) is equal to 55.

Note: Alternative solution : Given, cosec θ=5\text{cosec}\ \theta = 5. Here we need to find sec⁡(90o−θ)\sec(90^{o} - \theta). We know that Cosecant function is the reciprocal of sine function.
cosec θ=5\text{cosec}\ \theta = 5
⇒1sin⁡θ=5\Rightarrow \dfrac{1}{\sin\theta} = 5
Thus sin⁡ θ=15\sin\ \theta = \dfrac{1}{5}
Also we know that secant function is the reciprocal of the cosine function.
sec⁡(90o−θ) =1cos⁡(90o−θ)\sec(90^{o} - \theta)\ = \dfrac{1}{\cos\left( 90^{o} - \theta \right)}
We know that cos⁡(90o−θ)=sin⁡ θ\cos(90^{o} - \theta) = \sin\ \theta
sec⁡(90o−θ)=1sin⁡θ\sec\left( 90^{o} - \theta \right) = \dfrac{1}{\sin\theta}
By substituting sin⁡ θ=15\sin\ \theta = \dfrac{1}{5}, We get,
sec⁡(90o−θ)=1(15)\sec\left( 90^{o} - \theta \right) = \dfrac{1}{\left( \dfrac{1}{5} \right)}
On simplifying,
We get,
sec⁡(90o−θ) = 5\sec(90^{o} - \theta)\ = \ 5
Thus the value of sec⁡(90o−θ)\sec(90^{o} - \theta) is equal to 55.