Solveeit Logo
Login

Question

Question: How do you use a triple integral to find the volume of the given tetrahedron enclosed by the coordin...

How do you use a triple integral to find the volume of the given tetrahedron enclosed by the coordinate planes 2x+y+z=32x + y + z = 3 ?

Explanation

Solution

To do this question with the help of triple integral, first you have to integrate one variable by taking limits in terms of other two variables. When we go for the second integral only one variable left which we can put on limits and on third time integration there would be no variable on the constant left.

Complete step by step solution:
In the given question, we have
The equation of coordinate planes is 2x+y+z=32x + y + z = 3.
We can also write it as z=3−2x−yz = 3 - 2x - y .
Now, by setting z=0z = 0 , we know that it cuts the x-y plane to 2x+y=32x + y = 3.
By setting (x,y) = 0\left( {x,y} \right)\, = \,0, we know that the plane hits the z axis at z = 3 = \,3.
Similarly, it hits the x axis at x = 32x\, = \,\dfrac{3}{2}and y axis at y = 3y\, = \,3
So, we can draw it in the first octant

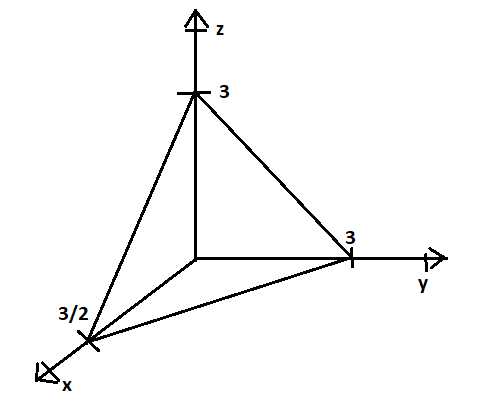
Now, we can put the limits as follows z=0  to  z= 3−2x−yz = 0\,\,to\,\,z = \,3 - 2x - y
y=0  to  y=3−2xy = 0\,\,to\,\,y = 3 - 2x
x = 0  to  x=32x\, = \,0\,\,to\,\,x = \dfrac{3}{2}
The triple integral is
⇒∫x=032∫y=03−2x∫z=03−2x−ydzdydx\Rightarrow \int\limits_{x = 0}^{\dfrac{3}{2}} {\int\limits_{y = 0}^{3 - 2x} {\int\limits_{z = 0}^{3 - 2x - y} {dzdydx} } }
=∫x=032∫y=03−2x[z]03−2x−ydydx=\int\limits_{x = 0}^{\dfrac{3}{2}} {\int\limits_{y = 0}^{3 - 2x} {\left[ z \right]_0^{3 - 2x - y}} } dydx
=∫x=032∫y=03−2x(3−2x−y)dydx= \int\limits_{x = 0}^{\dfrac{3}{2}} {\int\limits_{y = 0}^{3 - 2x} {\left( {3 - 2x - y} \right)} } dydx
=∫x=032(3y−2xy−y22)03−2xdx= \int\limits_{x = 0}^{\dfrac{3}{2}} {\left( {3y - 2xy - \dfrac{{{y^2}}}{2}} \right)} _0^{3 - 2x}dx
=∫x=032[3(3−2x)−2x(3−2x)−(3−2x)22]−[3(0)−2x(0)−(0)22]dx= \int\limits_{x = 0}^{\dfrac{3}{2}} {\left[ {3\left( {3 - 2x} \right) - 2x\left( {3 - 2x} \right) - \dfrac{{{{\left( {3 - 2x} \right)}^2}}}{2}} \right] - } \left[ {3\left( 0 \right) - 2x\left( 0 \right) - \dfrac{{{{\left( 0 \right)}^2}}}{2}} \right]dx
=∫032(9−6x−6x+4x2−9+4x2−12x2)dx= \int\limits_0^{\dfrac{3}{2}} {\left( {9 - 6x - 6x + 4{x^2} - \dfrac{{9 + 4{x^2} - 12x}}{2}} \right)dx}
=12∫032(18−24x+8x2−9−4x2+12x)dx= \dfrac{1}{2}\int\limits_0^{\dfrac{3}{2}} {\left( {18 - 24x + 8{x^2} - 9 - 4{x^2} + 12x} \right)dx}
=12(18x−24x22+8x33−9x−4x33+12x22)032= \dfrac{1}{2}\left( {18x - \dfrac{{24{x^2}}}{2} + \dfrac{{8{x^3}}}{3} - 9x - \dfrac{{4{x^3}}}{3} + \dfrac{{12{x^2}}}{2}} \right)_0^{\dfrac{3}{2}}
=12(18(32)−12(32)2+83(32)3−9(32)−43(32)3+6(32)2)= \dfrac{1}{2}\left( {18\left( {\dfrac{3}{2}} \right) - 12{{\left( {\dfrac{3}{2}} \right)}^2} + \dfrac{8}{3}{{\left( {\dfrac{3}{2}} \right)}^3} - 9\left( {\dfrac{3}{2}} \right) - \dfrac{4}{3}{{\left( {\dfrac{3}{2}} \right)}^3} + 6{{\left( {\dfrac{3}{2}} \right)}^2}} \right)
=12(27−27+9−272−92+272)= \dfrac{1}{2}\left( {27 - 27 + 9 - \dfrac{{27}}{2} - \dfrac{9}{2} + \dfrac{{27}}{2}} \right)
=94= \dfrac{9}{4}
Therefore, the volume of tetrahedron is 94\dfrac{9}{4} cubic units.

Note: This is a very useful application of triple integral. We can easily find the volume of three-dimensional bodies using triple integration by knowing the limits from where to where they are varying. In triple integration when we solve the integral for one variable then we have to eliminate that variable in limits for further integration.