Question

How do you use a graphing calculator to find the sum of the geometric series $\sum{5{{(0.2)}^{n-1}}}$ from n=1 to 10?

Answer 1

In order to find the solution to this question, we will start by expressing the given expression as a function in terms of n. Then we will write the steps to get the required answer.

Complete step by step answer:
According to the question, we have been asked to find the sum of the geometric series $\sum{5{{(0.2)}^{n-1}}}$ where the values of n range between 1 to 10.
Now, to solve this, we will first start this question by expressing the equation as a function in terms of n.
Let us consider the function as f(n). Hence, we get the function as
$f\left( n \right)=\sum{5{{(0.2)}^{n-1}}}$
Now, to find its final value, we will start by opening the graphing calculator in our device.
As soon as we open our graphing calculator, we follow a few steps to get our answer.
Step 1- We first write the given expression as a function that $f\left( n \right)=\sum{5{{(0.2)}^{n-1}}}$ in the appropriate place.
Step 2- To write the expression, we will represent ∑ by sum.
Step 3- As we will type sum, a list will appear with 5 options, that are

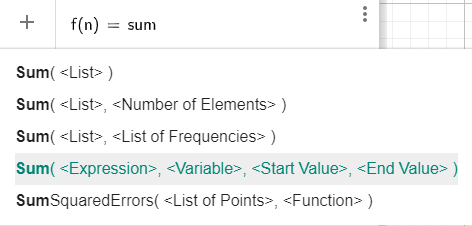
From these 5 options, we will check for the most suitable option according to our given situation.
Step 4- According to our question, we can see the choice 4 will be the more appropriate option to choose, that is Sum(, , , ).
Step 5- Now, we will put the asked value in the chosen option and press the enter key. As soon as we press, we will get our answer.

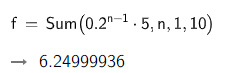
Note:
If we do not want to use a graphing calculator, then we can solve this question, using the formula of the sum of geometric series, that is ${{S}_{n}}=a\dfrac{({{r}^{n}}-1)}{(r-1)}$. And then by calculating values of a and r, we will get our answer. And then we can verify our answer using the graphing calculator.